この講義では、教科書の第6章「2つの平均値を比較する」をとりあげます。
具体的には、2つの平均値を比較する方法の学習、つまり、
(1)独立な2群の平均値差の検定と、(2)対応のある2群の平均値差の検定、
について学びます。
2群が
独立である具体的な例:
男女それぞれの心理学テストの成績、統計が好きな人と嫌いな人それぞれの統計学テストの成績、というように
2群がそれぞれ別々の標本から得られたデータが対象---
t検定を実施するための条件については、あとで述べる
t検定の前提条件を参照のこと
平均がそれぞれμ1、μ2、かつ分散σ2が等しい、正規分布に従う母集団から無作為抽出された標本X1、X2を考える:式で書くと X1~N (μ1, σ2) ,
X2~N (μ2,σ2)
その平均値の差(n1とn2はそれぞれの群のサンプルサイズ)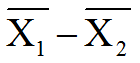 はやはり正規分布に従う:
はやはり正規分布に従う: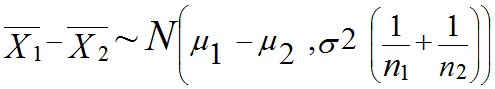
これを標準化する(問題: 標準化とは?):
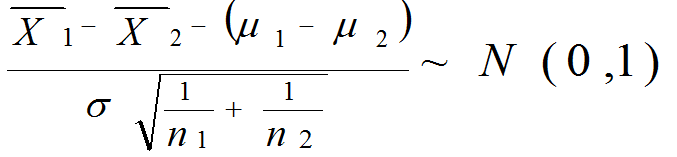
ここで母分散σ2が未知であるなら標本から推定する:
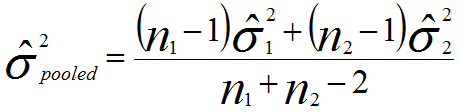 (ここで、
(ここで、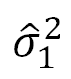 と
と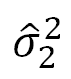 はそれぞれの群の不偏分散
---問題:X1とX2
を合わせた標本の不偏分散の値とこのσ2pooledとの関係は?)
はそれぞれの群の不偏分散
---問題:X1とX2
を合わせた標本の不偏分散の値とこのσ2pooledとの関係は?)
この値によって次の検定統計量を導く: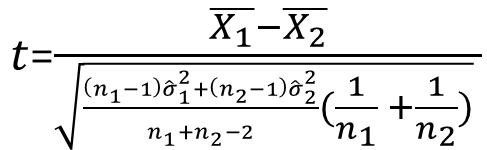
こうして導かれた検定統計量tの標本分布は、帰無仮説H0:μ1 = μ2のもとで、
自由度df = n1 + n2 - 2のt分布にしたがう。この検定統計量を用いて、2つの平均値の差に関する検定を行うことができるようになる(問題: 対立仮説はどうなる?):
例題:「統計テスト1」の得点の平均値に男女で有意な差があるかどうかを 有意水準5%、両側検定で検定せよ
統計1男 <- c(6,10,6,10,5,3,5,9,3,3)
統計1女 <- c(11,6,11,9,7,5,8,7,7,9)
次のステップで行う:
- 帰無仮説と対立仮説をたてる: 帰無仮説 H0: μ1 = μ2 (2つの母平均は等しい)
対立仮説 H1: μ1 ≠ μ2 (2つの母平均は等しくない)
- 検定統計量の選択:
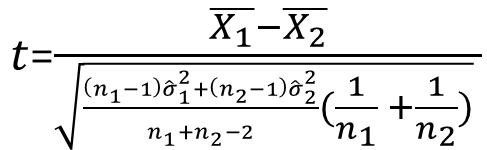 を検定統計量とする。これは、自由度 df = n1 + n2 - 2 のt分布に従う
を検定統計量とする。これは、自由度 df = n1 + n2 - 2 のt分布に従う
- 有意水準の決定: 両側検定で、有意水準 5%、つまりα=0.05
- 検定統計量の実現値の計算:
まず、2つの標本の平均と不偏分散を求め、
> mean(統計1男)
[1] 6
> mean(統計1女)
[1] 8
> var(統計1男)
[1] 7.777778
> var(統計1女)
[1] 4
次に「プール標準偏差」σpooled を求める。
> プール標準偏差<-sqrt(((length(統計1男)-1)*var(統計1男)+(length(統計1女)-1)*var(統計1女))/
(length(統計1男)+length(統計1女)-2))
> プール標準偏差
[1] 2.426703
最後に検定統計量の実現値を計算する:
> t分母 <- プール標準偏差*sqrt(1/length(統計1男)+1/length(統計1女))
> t分子 <- mean(統計1男)-mean(統計1女)
> ( t統計量 <- t分子/t分母 )
[1] -1.842885
検定統計量の実現値がt = -1.84と求まった
- 帰無仮説の棄却か採択かの決定: 帰無仮説によればこの検定統計量は自由度df=10+10-2=18のt分布に従う。
有意水準は5%、両側検定の時の棄却域を求める
> qt(0.025,18)
[1] -2.100922
> qt(0.025,18,lower.tail=FALSE)
[1] 2.100922
この結果、棄却域は t < -2.10 または t > 2.10 となるので、tの値は棄却域に入らないため、帰無仮説は棄却されない。ゆえに、検定の結果は「有意水準5%で有意差が見られなかった」となる
関数 pt を用いて、直接p値を求めることもできる:
> pt(-1.842885,18)
[1] 0.04093903
> 2*pt(-1.842885,18)
[1] 0.08187807
なお、5章「t分布を用いた検定」で紹介した関数t.testによっても簡単に求めることができる(var.equal=TRUEというオプションをつける):
> t.test(統計1男,統計1女,var.equal=TRUE)
Two Sample t-test
data: 統計1男 and 統計1女
t = -1.8429, df = 18, p-value = 0.08188
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-4.2800355 0.2800355
sample estimates:
mean of x mean of y
6 8
2群の分散が等しいことを「この2群の分散は等質である」といいます。t検定では2群の分散が等質であることが前提です。それには「分散の等質性の検定」を行う必要があります。そして、Rではvar.test関数で行えます(検定統計量をFとしています):
> クラスA <- c(54,55,52,48,50,38,41,40,53,52)
> クラスB<- c(67,63,50,60,61,69,43,58,36,29)
> var.test(クラスA, クラスB)
F test to compare two variances
data: クラスA and クラスB
F = 0.2157, num df = 9, denom df = 9, p-value = 0.03206
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.05356961 0.86828987
sample estimates:
ratio of variances
0.2156709
この例では、p値が 0.03であるため、帰無仮説が棄却されます。
つまりこの例では2つの変数の分散が等質であるという仮定は成り立ちません。そのため、この2つの変数に対してはt検定ができない、ということになります。その場合でも2つの群の平均値の比較の検定は可能です。その一つの方法が、次で紹介するWelchの検定です。
[
なぜ分散が等質でないと判断されたか]
今の説明で「p値が 0.03であるため、帰無仮説が棄却された
(つまりこの例では2つの変数の分散が等質であるという仮定は成り立たない)」
という点に疑問を持った人のために、解説します。
var.testが行ったのは、「2つの群が等質である」ことの検定を行ったのではないのです。行ったのは「等質でない」(これが『対立仮説』、帰無仮説は「等質である」)ことの検定でした。
そして有意水準を5%とすると、p<0.05ですから、帰無仮説が棄却され、対立仮説が採択されたのです。つまり、
「この例では2つの変数の分散が等質であるという仮定は成り立たない」という結論になります。
Welchの検定
母分散が等質でないときは、t検定は使えないのでWelch検定を使う---Rのt.test関数で、
var.equal=FALSEというオプションをつける(var.equalオプションを略してもよい)
> t.test(クラスA, クラスB, var.equal=FALSE)
Welch Two Sample t-test
data: クラスA and クラスB
t = -1.1191, df = 12.71, p-value = 0.2838
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-15.554888 4.954888
sample estimates:
mean of x mean of y
48.3 53.6
この結果はp値が0.28なので、帰無仮説が棄却されない、つまりクラスAとクラスBの平均に有意な差はない、という結論。
課題5-3
Rを使った実習(教科書pp.143-147)の例題のデータ、統計1男と統計1女のデータに対して、分散の等質性の検定を行え。また分散の等質性が成り立たないと仮定してWelchの検定を行い、その結果を前の例題の結果と比較せよ。
- 対応のあるデータ: 例えば、同じ被験者について複数の測定が行われている場合
例: 統計の指導を受ける前と後のテスト得点である「統計テスト1」と「統計テスト2」
対応あるデータについては、独立な2群のt検定ではない別の方法が必要
対応のあるデータでは「
変化量(あるいは差得)」を考える。
統計テスト1の得点をX
1、統計テスト2の得点をX
2、変化量(差得点)をDとすれば
D = X2 - X1
さらに、これらの標本平均
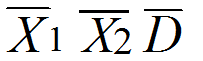
の間には
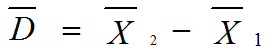
という関係がなりたつ。
差得点D ~ N (μD, σ2D) と仮定すると、
標本平均 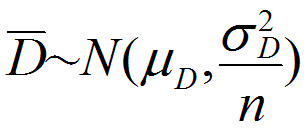
この標本分布を標準化すると 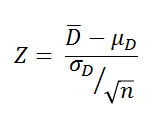 ~ N (0, 1)
~ N (0, 1)
ここで、σDが未知なので、これを標本から求めた標準偏差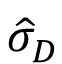 で代用すると、
で代用すると、
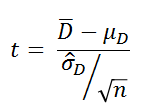 は自由度 df = n - 1
のt分布にしたがう
は自由度 df = n - 1
のt分布にしたがう
例題:指導の前後に行った「統計テスト1」と「統計テスト2」で有意な差があるかどうかを 有意水準5%、両側検定で検定せよ
統計テスト1 <- c(6,10,6,10,5,3,5,9,3,3,11,6,11,9,7,5,8,7,7,9)
統計テスト2 <- c(10,13,8,15,8,6,9,10,7,3,18,14,18,11,12,5,7,12,7,7)
次のステップで行う:
- 帰無仮説と対立仮説をたてる: 帰無仮説 H0: μD = 0 (2つのテストの差の母平均は0)
対立仮説 H1: μD ≠ 0 (2つのテストの差の母平均は0) ではない)
- 検定統計量の選択:
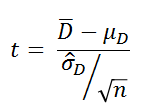 を検定統計量とする(帰無仮説の下ではμD = 0なので、
を検定統計量とする(帰無仮説の下ではμD = 0なので、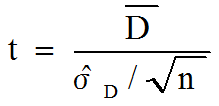 )。これは、自由度 df = n-1 のt分布に従う
)。これは、自由度 df = n-1 のt分布に従う
- 有意水準の決定: 両側検定で、有意水準 5%、つまりα=0.05
- 検定統計量の実現値の計算:
> 変化量 <- 統計テスト2-統計テスト1
> sd(変化量)
[1] 2.772041
> 分母t <-sd(変化量)/sqrt(length(変化量))
> 分子t <- mean(変化量)
> t統計量 <- 分子t/分母t
> t統計量
[1] 4.839903
この結果、検定統計量の実現値は t= 4.84
- 帰無仮説の棄却か採択かの決定: 帰無仮説によればこの検定統計量は自由度df=20-1=19のt分布に従う。
有意水準は5%、両側検定の時の棄却域を求める
> qt(0.025,19)
[1] -2.093024
> qt(0.025,19,lower.tail=FALSE)
[1] 2.093024
この結果、棄却域は t < -2.09 または t > 2.09 となるので、tの値は棄却域に入るため、帰無仮説は棄却される。ゆえに、検定の結果は「5%水準で有意差が見られた」となる
なお、t.test関数にオプション paired=TRUEを指定することでも対応のあるt検定を求めることができる:
> t.test(統計テスト1, 統計テスト2, paired=TRUE)
Paired t-test
data: 統計テスト1 and 統計テスト2
t = -4.8399, df = 19, p-value = 0.0001138
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-4.297355 -1.702645
sample estimates:
mean of the differences
-3
この結果、p値が0.0001という小さな値であるので、帰無仮説が棄却され、検
定の結果は「有意水準5%で、統計テスト1と統計テスト2では有意な差があった」となる。
| 目的 |
関数名と書式 |
使い方 |
| 分散の等質性の検定 |
var.test(x1, x2)
| var.test(x1, x2)
⇒ 変数x1とx2(これは同一の変数xについてグループ1とグループ2の得点)について、分散の等質性の検定を行う
|
| 独立な2群の検定 |
t.test(x1, x2, var.equal=TRUE)
| t.test(x1, x2, var.equal=TRUE)
⇒ 変数x1とx2(これは同一の変数xについてグループ1とグループ2の得点)について、
独立な2群のt検定を行う。var.equal=TRUEがないとWelchの検定になる
|
| Welchの検定 |
var.test(x1, x2, var.equal=FALSE)
| var.test(x1, x2, var.equal=FALSE)
⇒ 変数x1とx2(これは同一の変数xについてグループ1とグループ2の得点)について、分散の等質性を仮定せずに独立な2群のt検定を行う. var.equal=FALSE により
「分散の等質性が仮定されない」
|
| 対応のあるt検定 |
t.test(x) あるいは
t.test(x1, x2, paired=TRUE)
| t.test(x)
⇒ 変数xについて、1つの平均値のt検定を実行する。xが2変数の差得点(x = x1 - x2)であれば、対応のあるt検定を行ったことになる
t.test(x1,x2,paired=TRUE)
⇒ paired=TRUEにより、x1, x2が対応のあるデータとして、対応のあるt検定を行う
|
問題(1): 教科書」p.158 (1)
以下は、統計学が好きな人の得点と嫌いな人の得点のデータである。統計学が好きか嫌いかという2群について、平均値に有意な差があるかどうかを、有意水準5%の両側検定で調べよ。
統計学好き <- c(6, 10, 6, 10, 11, 6, 11, 7)
統計学嫌い <- c(5, 3, 5, 9, 3, 3, 9, 5, 8, 7, 7, 9)
[
ヒント]
「統計学好き」と「統計学嫌い」の2変数は、分散が等質かどうか不明である。そこで、まず(1)分散の等質性の検定を行い、
その結果(2a)分散が等質であればt検定を行い、(2b)分散が等質でなければWelchの検定を行う。
問題(2): 教科書」p.158 (2)
以下は、心理学テストにおける、男と女のデータである。男女で平均値に有意な差があるかどうかを、有意水準5%の両側検定で調べよ。
心理学テスト男 <- c(13, 14, 7, 12, 10, 6, 8, 15, 4, 14)
心理学テスト女 <- c(9, 6, 10, 12, 5, 12, 8, 8, 12, 15)
[
ヒント]
「心理学テスト男」と「心理学テスト女」の2変数は、分散が等質かどうか不明である。そこで、まず(1)分散の等質性の検定を行い、
その結果(2a)分散が等質であればt検定を行い、(2b)分散が等質でなければWelchの検定を行う。
問題(3) : 教科書」p.158 (3)
以下はビデオ視聴によるダイエットプログラムに参加した10名の、プログラム参加前後の体重のデータである(単位はkg)。
このデータから、ダイエットプログラムは効果があったと言えるかどうかを判定せよ。有意水準を5%、両側検定とする。
参加前 <- c(61, 50, 41, 55, 51, 48, 46, 55, 65, 70)
参加後 <- c(59, 48, 33, 54, 47, 52, 38, 50, 64, 63)
[
ヒント]
同じ人についてのプログラム参加前と後のデータなので、「対応のあるt検定」を行う。
問題(4)
shidouhou.csvは区切り記号がコンマのCSV形式のファイルであり、教科書p.38-39のデータが収められている。
このデータをデータフレームとして読み込み、統計テスト1と心理学テストの母平均に差があるかどうか、検定を行え。
[
参考: csvファイルを読み込む]
区切り記号がコンマのcsvファイルを読み込み、その内容をデータフレームとして取り込むには、
read.csv関数を用いる。
もっとも中にはちゃんと読み込めないこともあるので、値を確認すること。
そして読み込めない場合は、区切り記号を適切なものにセットしたり、
他の read.table というような関数を使ってみることも考えよう。
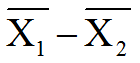 はやはり正規分布に従う:
はやはり正規分布に従う: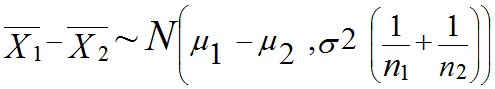
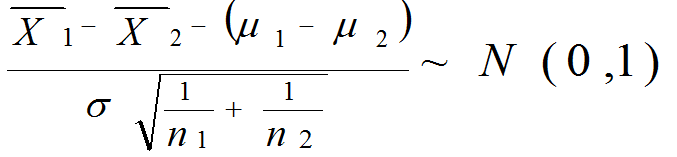
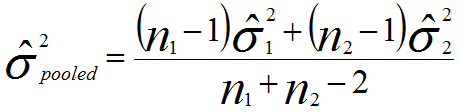 (ここで、
(ここで、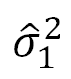 と
と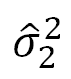 はそれぞれの群の不偏分散
---問題:X1とX2
を合わせた標本の不偏分散の値とこのσ2pooledとの関係は?)
はそれぞれの群の不偏分散
---問題:X1とX2
を合わせた標本の不偏分散の値とこのσ2pooledとの関係は?)
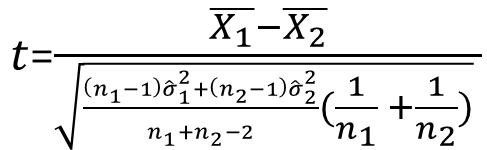
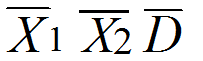 の間には
の間には
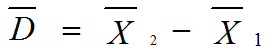 という関係がなりたつ。
という関係がなりたつ。
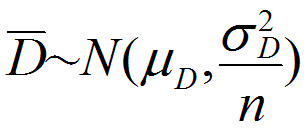
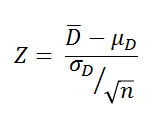 ~ N (0, 1)
~ N (0, 1)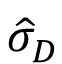 で代用すると、
で代用すると、
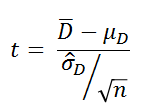 は自由度 df = n - 1
のt分布にしたがう
は自由度 df = n - 1
のt分布にしたがう
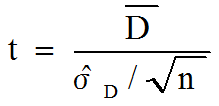 )。これは、自由度 df = n-1 のt分布に従う
)。これは、自由度 df = n-1 のt分布に従う