画像から特徴を抽出した後は、いろいろな画像に現れる特徴をマッチングする(対応付ける)こと。マッチングにおける重要点は、マッチングした特徴の集合が幾何学的な一貫性をもっているかどうかということ。
幾何学的な画像位置合わせ(geometric image registration)、つまりある画像から別な画像へ特徴を変換する2次元と3次元の変換計算。
カメラの姿勢推定やカメラのキャリブレーション(内部パラメタの推定)
最小2乗法を用いた2次元位置合わせ¶
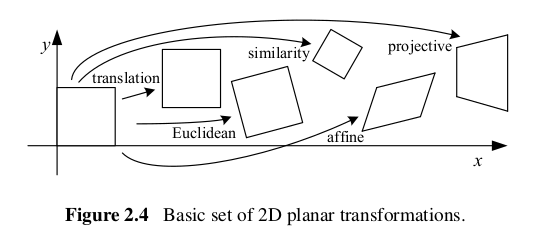
基本的な2次元幾何変換
対応する複数の特徴点$\{(\boldsymbol{x}_i, \boldsymbol{x}'_i)\}$と平面パラメトリック変換 $\boldsymbol{x}'=\boldsymbol{f}(\boldsymbol{x};\boldsymbol{p})$が与えられた時、 残差の2乗和を最小化する$\boldsymbol{p}$を最も良い運動パラメタと推定する: $\displaystyle E_{LS} = \sum_{i}\| \boldsymbol{r}_i \|^2 = \sum_{i}\| \boldsymbol{f}(\boldsymbol{x}_i;\boldsymbol{p})-\boldsymbol{x}'_i\|^2 $
ここで$\boldsymbol{r}_i = \boldsymbol{x}'_i-\boldsymbol{f}(\boldsymbol{x}_i;\boldsymbol{p}) =\hat{\boldsymbol{x}}'_i- \tilde{\boldsymbol{x}}'$は、観測された位置$\hat{\boldsymbol{x}}'_i$とその予測位置$\tilde{\boldsymbol{x}}'_i=\boldsymbol{f}(\boldsymbol{x}_i;\boldsymbol{p}) $の残差。
下記の表の多くの変換モデル(=運動モデル)、つまり並進、相似、アフィンは移動量$\Delta\boldsymbol{x}=\boldsymbol{x}'-\boldsymbol{x}$とパラメタ$\boldsymbol{p}$の関係が線形
$\Delta\boldsymbol{x}=\boldsymbol{x}'-\boldsymbol{x}=\boldsymbol{J}(\boldsymbol{x})\boldsymbol{p}$
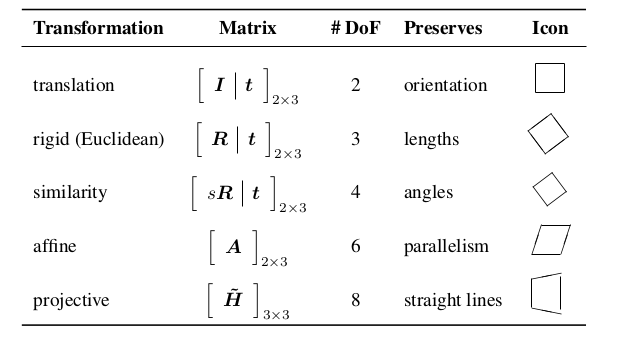
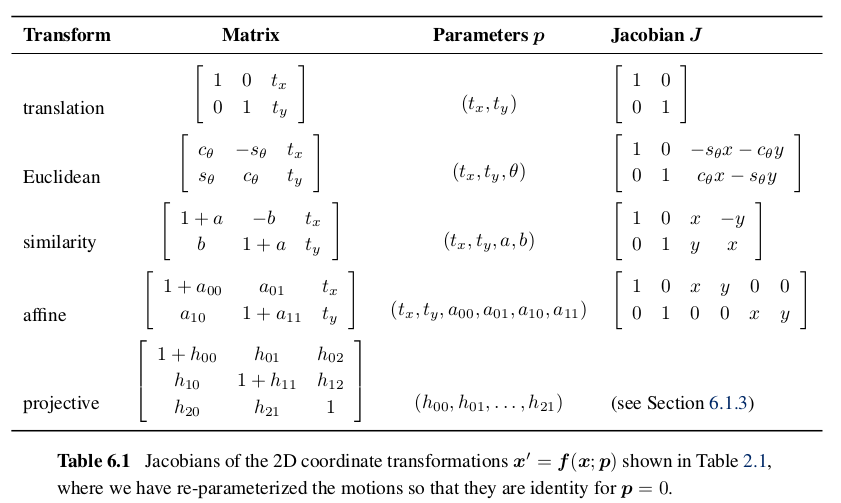
ここで$\boldsymbol{J}=\partial \boldsymbol{f}/\partial \boldsymbol{p}$はパラメタ$\boldsymbol{p}$に関する変換$\boldsymbol{f}$のヤコビ行列。これを用いて最小2乗問題は以下のように表される:
$\displaystyle E_{LS} = \sum_{i} \| \boldsymbol{J}(\boldsymbol{x}_i)\boldsymbol{p} - \Delta\boldsymbol{x}_i \|^2=\boldsymbol{p}^T\left[ \sum_{i}\boldsymbol{J}^T(\boldsymbol{x}_i)\boldsymbol{J}(\boldsymbol{x}_i)\right] \boldsymbol{p}- 2\boldsymbol{p}^T\left[ \sum_{i}\boldsymbol{J}^T(\boldsymbol{x}_i)\Delta\boldsymbol{x}_i\right] +\sum_i \|\Delta\boldsymbol{x}_i\|^2 = \boldsymbol{p}^T\boldsymbol{A}\boldsymbol{p} -2\boldsymbol{p}^T\boldsymbol{b}+c$
この最小値は正規方程式 $ \boldsymbol{Ap}=\boldsymbol{b}$ を解いて得られる。ここで$\boldsymbol{A}=\sum_{i}\boldsymbol{J}^T(\boldsymbol{x}_i)\boldsymbol{J}(\boldsymbol{x}_i)$は正定値対称行列で、ヘッセ行列と呼ばれる。また$\boldsymbol{b}=\sum_{i}\boldsymbol{J}^T(\boldsymbol{x}_i)\Delta\boldsymbol{x}_i$
回転のない並進運動の場合は、この方程式の解は対応点間の並進運動の平均、という単純な解
不確実性の重み付け¶
先の最小二乗法ではすべての特徴点が同じ精度で対応付けられていると仮定。しかし実際にはこの仮定は不成立。
重み付き最小二乗法: それぞれの対応点に分散の推定値$\sigma^2$という重みをつける。 $E_{WLS}=\sum_i \sigma_i^{-2}\|\boldsymbol{r}_i\|^2$
反復アルゴリズム¶
測定値と未知数が線形な関係でない場合は『線形』最小二乗法ではなく、「非線形」最小二乗法もしくは非線形回帰の問題
例:2つの点集合から2次元剛体ユークリッド変換(並進と回転)を推定する場合。ヤコビ行列が$\theta$に依存する。
非線形最小二乗法では、以下の最小化を求めることで、反復的に$\Delta\boldsymbol{p}$を更新して、パラメタ$\boldsymbol{p}$を推定する:
$\begin{array}{lll}
E_{NLS}(\Delta\boldsymbol{p}) & = & \sum_{i}\| \boldsymbol{f}(\boldsymbol{x}_i;\boldsymbol{p}+\Delta\boldsymbol{p})-\boldsymbol{x}'_i\|^2 \\
& \approx & \sum_{i}\| \boldsymbol{J}(\boldsymbol{x}_i;\boldsymbol{p})\Delta\boldsymbol{p}-\boldsymbol{r}'_i\|^2 \\
& = & \Delta\boldsymbol{p}^T \left[ \sum_i \boldsymbol{J}^T \boldsymbol{J} \right]\Delta\boldsymbol{p} - 2\Delta\boldsymbol{p}^T\left[ \sum_i \boldsymbol{J}^T \boldsymbol{r}_i \right] + \sum_i \| \boldsymbol{r}_i \|^2 \\
& = & \Delta\boldsymbol{p}^T \boldsymbol{A} \Delta\boldsymbol{p} - 2 \Delta\boldsymbol{p}^T\boldsymbol{b} + c\\
\end{array}$
ここで$\boldsymbol{A}=\sum_{i}\boldsymbol{J}^T(\boldsymbol{x}_i)\boldsymbol{J}(\boldsymbol{x}_i)$はヘッセ行列(本来の非線形最小二乗法におけるヘッセ行列ではないことに注意)
$\boldsymbol{b}=\sum_{i}\boldsymbol{J}^T(\boldsymbol{x}_i)\boldsymbol{r}_i)$は残差ベクトルのヤコビ行列による重み付けされた和 --- ヤコビ行列に比例する強さで予測誤差の方向にパラメタが引っ張られている、という印象
$\boldsymbol{A}$と$\boldsymbol{b}$が求められたら、以下の式を用いて$\Delta\boldsymbol{p}$を計算し、$\boldsymbol{p}\leftarrow\boldsymbol{p}+\Delta\boldsymbol{p}$によって更新:
$(\boldsymbol{A}+\lambda \mathrm{diag}(\boldsymbol{A}))\Delta\boldsymbol{p} = \boldsymbol{b}$
この$\lambda$は一種のダンピング・パラメタで、降下ステップを保証するためのもの。
2次元の並進と回転の場合、未知数$(\delta t_x,\delta t_y,\delta \theta)$をもつ$3 \times 3$の正規方程式が得られる。$(\delta t_x,\delta t_y,\delta \theta)$の初期値は4パラメタ$(t_x,t_y,c,s)$としての相似変換にあてはめて$\theta=\tan^{-1}(s/c)$とすることで得られる。
他の変換については省略(出典文献を参照のこと)
ロバスト最小二乗法とRANSAC¶
特徴点の対応に外れ値がある場合、最小二乗法を頑健にした手法が必要。
M推定法: 残差の2乗ではなく、頑健なペナルティ関数$\rho(r)$を用いた次の式を用いる: $\displaystyle E_{RLS}(\Delta\boldsymbol{p}) = \sum_{i}\rho(\| \boldsymbol{r}_i \|)$ この関数を$\boldsymbol{p}$で微分し、右辺を0と置く(極値を求める)と、
$\displaystyle \sum_i \psi(\| \boldsymbol{r}_i \|)\frac{\partial \| \boldsymbol{r}_i\|)}{\partial \boldsymbol{p}} = \sum_i \frac{\psi(\| \boldsymbol{r}_i \|)}{\| \boldsymbol{r}_i\|} \boldsymbol{r}_i^T \frac{\partial \boldsymbol{r}_i}{\partial \boldsymbol{p}} = 0$
ここで$\psi(r)=\rho'(r)$は$\rho$の導関数で、影響関数と呼ばれる。
重み関数$w(r)=\psi(r)/r$を導入すると、上記は反復再重み付け最小二乗法$E_{IRLS}=\sum_i w(\| \boldsymbol{r}_i \|)\|\boldsymbol{r}_i\|^2$ を最小化することに等しい。
このとき$w(\| \boldsymbol{r}_i \|)$は$\|\boldsymbol{r}_i\|^2$に対する重み付けの役割
M推定法は外れ値が多いと、収束しない可能性がある
これに対する2つのアプローチ: RANSAC(random sample consensus)と最小二乗メディアン(least median of squares)
どちらも、$k$個の対応を部分集合として(ランダムに)選択することから始める。選択された対応は未知パラメタ$\boldsymbol{p}$の初期推定値の計算に利用する。そしてすべての対応集合に対する残差を計算する: $\boldsymbol{r}_i = \tilde{\boldsymbol{x}}'_i(\boldsymbol{x}_i;\boldsymbol{p})$$ - \hat{\boldsymbol{x}}'_i$
ここで$\tilde{\boldsymbol{x}}'_i$は推定された(変換後の)位置、$\hat{\boldsymbol{x}}'_i$は観測された特徴点位置
RANSACはこのあと、予測位置から$\epsilon$以内に存在するインライヤー(正しい値の候補)、つまり$\|\boldsymbol{r}_i\| \leq \epsilon$の個数を数える($\epsilon$の値はたいてい1から3)。 最小二乗メディアン(LMS)は$\|\boldsymbol{r}_i\|^2$の中央値を求める。
ランダム選択を$S$回繰り返し、RANSACでは最大インライヤー数、LMSでは最小メディアン残差をもつ部分集合を最終的な解候補とする。そしてこれを導いた、RANSACではパラメタ推定値$\boldsymbol{p}$、LMSではインライヤー集合を、この後のデータ当てはめの処理に渡す。
RANSACには、改良版のPreemptive RANSACやPROSACがある。
ランダムサンプリングを用いているため、十分な回数$S$の試行が必要。