基礎¶
2次元点¶
2次元空間上の点$\boldsymbol{x}$を列ベクトルで表す:$\displaystyle \boldsymbol{x} = \begin{bmatrix}x \\ y \end{bmatrix}$ --- これを$\boldsymbol{x} = (x \ y)^T =(x,y)$で表す
同次座標系 (参考: http://www.eli.hokkai-s-u.ac.jp/~kikuchi/ma2/chap10a.html) を用いて $\tilde{\boldsymbol{x}} = (\tilde{x}, \tilde{y},\tilde{z})$と表現し、同次ベクトルという。
この同次ベクトル$\tilde{\boldsymbol{x}}=(\tilde{x}, \tilde{y}, \tilde{w})$は、$\tilde{w}$で割ることで非同次ベクトル$\boldsymbol{x}$に戻せる: $\tilde{\boldsymbol{x}}= \tilde{w}(x, y, 1) = \tilde{w}\bar{\boldsymbol{x}}$
ここで$\bar{\boldsymbol{x}}=(x,y,1)$は拡張ベクトルという
2次元直線¶
同次座標系を用いて$\tilde{\boldsymbol{l}} = (a,b,c)$と表わせる。直線の方程式は $\bar{\boldsymbol{x}}\cdot\tilde{\boldsymbol{l}}=ax+by+c = 0$
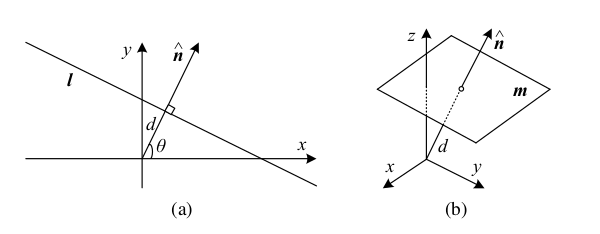
$\|\hat{\boldsymbol{n}}\| = 1$となるよう正規化して$\boldsymbol{l}=(\hat{\boldsymbol{n}}, d) = (\hat{n}_x, \hat{n}_y, d)$と表せる(ただしこれができない例外は、無限遠直線$(0,0,1)$)。このとき、$\hat{\boldsymbol{n}}$はこの直線に直交する法線ベクトル、$d$は原点から直線までの距離。
$\hat{\boldsymbol{n}}$を回転角$\theta$の関数$\hat{\boldsymbol{n}}=(\hat{n}_x,\hat{n}_y)=(\cos\theta,\sin\theta)$として表すことができる。この$(\theta,d)$は極座標表現という。
同次座標系を用いると2つの直線$\tilde{\boldsymbol{l}}_1$と$\tilde{\boldsymbol{l}}_2$の交点は$\tilde{\boldsymbol{x}}=\tilde{\boldsymbol{l}}_1 \times \tilde{\boldsymbol{l}}_2$と表せる($\times$は外積)。
また2点($\tilde{\boldsymbol{x}}_1$, $\tilde{\boldsymbol{x}}_2$)を通る直線は $\tilde{\boldsymbol{l}}=\tilde{\boldsymbol{x}}_1 \times \tilde{\boldsymbol{x}}_2$と表せる。
2次元円錐曲線¶
円錐曲線は多項式の同次表現で表されるものの一つ。2次形式を用いて$\tilde{\boldsymbol{x}}^T \boldsymbol{Q}\tilde{\boldsymbol{x}} = 0$
3次元点¶
3次元空間における点は、非同次座標系では$\boldsymbol{x}=(x,y,z)$、同次座標系では$\tilde{\boldsymbol{x}}=(\tilde{x},\tilde{y},\tilde{z},\tilde{w})$と表される。2次元点と同様に拡張ベクトル$\bar{\boldsymbol{x}}=(x,y,z,1)$を用いて$\tilde{\boldsymbol{x}}=\tilde{w}\bar{\boldsymbol{x}}$と表せる。
3次元平面¶
2次元平面と同様に、同次座標系$\tilde{\boldsymbol{m}}=(a,b,c,d)$を用いて表わせ、方程式 $\bar{\boldsymbol{x}}\cdot\tilde{\boldsymbol{m}}=ax+by+cz+d=0$ によって表現できる。
これも$\|\hat{\boldsymbol{n}}\| = 1$となるよう正規化して$\boldsymbol{m}=(\hat{\boldsymbol{n}}, d) = (\hat{n}_x, \hat{n}y, \hat{n}_z,d)$と表せる(ただしこれができない例外は、無限遠平面$(0,0,0,1)$)。このとき、$\hat{\boldsymbol{n}}$はこの平面に直交する法線ベクトル、$d$は原点から平面までの距離。
$\hat{\boldsymbol{n}}$を2つの回転角$\theta, \phi$の関数$\hat{\boldsymbol{n}}=(\cos\theta\cos\phi,\sin\theta\cos\phi, \sin\phi)$として表すことができる。これは球面座標という。
3次元直線¶
3次元の点$(\boldsymbol{p}, \boldsymbol{q})$を通る直線上の任意の点$\boldsymbol{r}$は次で表現できる。 $\boldsymbol{r} = (1 - \lambda)\boldsymbol{p}+ \lambda \boldsymbol{q}$。ここで$0 \geq \lambda \geq 1$とするとこれは$\boldsymbol{p}$と$\boldsymbol{q}$を通る線分上の点を表す。
同次表現を用いると$\tilde{\boldsymbol{r}}=\mu \tilde{\boldsymbol{p}}+ \lambda \tilde{ \boldsymbol{q}}$と表せる。
$\tilde{\boldsymbol{q}}$を無限遠点、つまり$(\tilde{d}_x,\tilde{d}_y,\tilde{d}_z,0)=(\tilde{\boldsymbol{d}},0)$にとったとき、$\tilde{\boldsymbol{d}}$を直線の向きとみなせる。 直線の非同次表現は$\boldsymbol{r}=\boldsymbol{p}+\lambda\tilde{\boldsymbol{d}}$と書ける。
ただしこれでは自由度が多すぎる(3次元直線は本来自由度が4、それに対し上の表現では6)
Plücker座標: $\boldsymbol{L}=\tilde{\boldsymbol{p}}\tilde{\boldsymbol{q}}^T - \tilde{\boldsymbol{q}}\tilde{\boldsymbol{p}}^T$
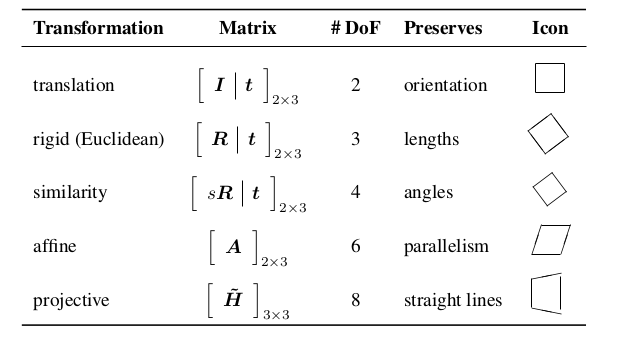
2次元変換¶
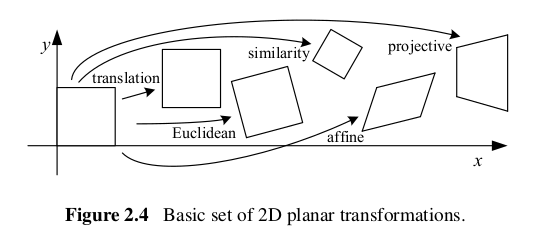
並進(translation)¶
2次元の点$\boldsymbol{x}$を$\boldsymbol{t}$だけ並進させた点$\boldsymbol{x'}$は次で表される: $\displaystyle \boldsymbol{x'}=\boldsymbol{x}+\boldsymbol{t}$ または $\boldsymbol{x'}=\begin{bmatrix}\boldsymbol{I} & \boldsymbol{t}\end{bmatrix} \bar{\boldsymbol{x}}$
ここで$\boldsymbol{I}$は$2\times 2$の単位行列、だから上は$2\times 3$行列。また$\boldsymbol{0}$を零ベクトルとすると、
$\bar{\boldsymbol{x'}} = \begin{bmatrix}\boldsymbol{I} & \boldsymbol{t}\\ \boldsymbol{0}^T & 1 \end{bmatrix} \bar{\boldsymbol{x}}$ とも表され、これは$3 \times 3$行列。
回転(rotation)と並進¶
2次元剛体運動(2D rigid body motion)とか、2次元ユークリッド変換(2D Euclid transformation)とも呼ばれる
$\displaystyle \boldsymbol{x'}=\boldsymbol{Rx}+\boldsymbol{t}$ または $\boldsymbol{x'}=\begin{bmatrix}\boldsymbol{R} & \boldsymbol{t}\end{bmatrix} \bar{\boldsymbol{x}}$
ここで$\boldsymbol{R} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}$ は、$\boldsymbol{R}\boldsymbol{R}^T=\boldsymbol{I}$かつ$|\boldsymbol{R}|=1$となる正規直交回転行列
スケール(scale)と回転と並進¶
相似変換(similarity transformation)とも呼ばれ、2つの直線がなす角度が保存される。
任意のスケール$s$を用いて $\boldsymbol{x'}=s\boldsymbol{Rx}+\boldsymbol{t}$と表される。
また $\boldsymbol{x'} = \begin{bmatrix} s\boldsymbol{R} & \boldsymbol{t} \end{bmatrix} \bar{\boldsymbol{x}}$$ = \begin{bmatrix} a & -b & t_x \\ b & a & t_y \end{bmatrix}\bar{\boldsymbol{x}} $ とも表される
アフィン変換(affine trnsformation)¶
平行な直線は変換後も平行なままになる。$\boldsymbol{x'}=\boldsymbol{A\bar{x}}$で表される。ここで $\boldsymbol{A}$は$2 \times 3$行列で、$\boldsymbol{x'}=\begin{bmatrix}a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \end{bmatrix}\bar{\boldsymbol{x}}$
射影変換(projective transformation)¶
直線を保存する変換で、透視変換(perspective transformation)ともホモグラフィ(homography, 平面射影変換)ともいう。
同次座標系において $\boldsymbol{\tilde{x}'} = \tilde{\boldsymbol{H}} \boldsymbol{\tilde{x}}$で表される。 ここで$\tilde{\boldsymbol{H}}$は任意の$3 \times 3$行列で同次行列。
3次元変換¶
2次元変換に似て、それぞれの変換は階層の関係にある。
並進(translation)¶
3次元の点$\boldsymbol{x}$の並進移動は次で表される: $\displaystyle \boldsymbol{x'}=\boldsymbol{x}+\boldsymbol{t}$ または $\boldsymbol{x'}=\begin{bmatrix}\boldsymbol{I} & \boldsymbol{t}\end{bmatrix} \bar{\boldsymbol{x}}$
ここで$\boldsymbol{I}$は$3\times 3$の単位行列
回転と並進(rotation and translation)¶
3次元剛体運動(3D rigid body motion)とか、3次元ユークリッド変換(3D Euclid transformation)とも呼ばれる
$\displaystyle \boldsymbol{x'}=\boldsymbol{Rx}+\boldsymbol{t}$ または $\boldsymbol{x'}=\begin{bmatrix}\boldsymbol{R} & \boldsymbol{t}\end{bmatrix} \bar{\boldsymbol{x}}$
ここで$\boldsymbol{R}$は$3 \times 3$の正規直交回転行列、$\boldsymbol{R}\boldsymbol{R}^T = \boldsymbol{I}$ かつ$| \boldsymbol{R} |=1$を満たす。
$\boldsymbol{x'}= \boldsymbol{R}(\boldsymbol{x}- \boldsymbol{c}) = \boldsymbol{Rx} - \boldsymbol{Rc} $とも表される。このとき$\boldsymbol{c}$は回転中心。
スケール(scale)と回転と並進¶
3次元相似変換(3D similarity transformation)とも呼ばれ、2つの直線もしくは平面がなす角度が保存される。
任意のスケール$s$を用いて $\boldsymbol{x'}=s\boldsymbol{Rx}+\boldsymbol{t}$、もしくは $\boldsymbol{x'} = \begin{bmatrix} s\boldsymbol{R} & \boldsymbol{t} \end{bmatrix} \bar{\boldsymbol{x}}$と表される
アフィン変換(affine trnsformation)¶
平行な直線や平面は変換後も平行なままになる。$\boldsymbol{x'}=\boldsymbol{A\bar{x}}$で表される。ここで $\boldsymbol{A}$は$3 \times 4$行列で、 $\boldsymbol{x'}=\begin{bmatrix}a_{00} & a_{01} & a_{02} & a_{03} \\ a_{10} & a_{11} & a_{12} & a_{13} \\ a_{20} & a_{21} & a_{22} & a_{23} \end{bmatrix}\bar{\boldsymbol{x}}$
射影変換(projective transformation)¶
直線を保存する変換で、3次元透視変換(3D perspective transformation)ともホモグラフィ(homography)、共線写像(collineation)ともいう。
同次座標系において $\boldsymbol{\tilde{x}'} = \tilde{\boldsymbol{H}} \boldsymbol{\tilde{x}}$で表される。 ここで$\tilde{\boldsymbol{H}}$は任意の$4 \times 4$行列で同次行列。
3次元変換の関係¶
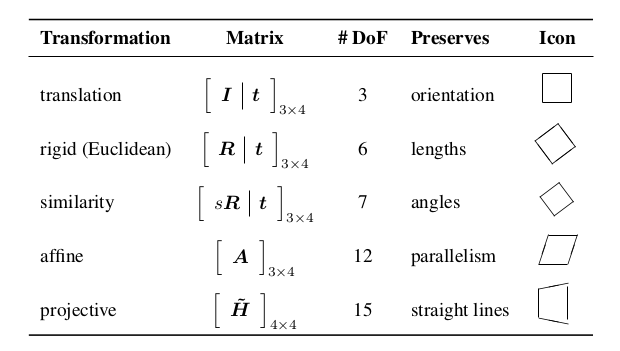
3次元回転¶
2次元座標変換と3次元座標変換の違い: 3次元回転行列$\boldsymbol{R}$のパラメタ表現に複数の表現方法が存在
- オイラー角
3つの座標軸周りの3つの回転の積で表現。ただしどの順番で回転させるかで結果が異なる、という問題あり 回転軸・回転角表現
回転軸$\hat{\boldsymbol{n}}$と回転角$\theta$、もしくは3次元ベクトル$\boldsymbol{\omega} = \theta\hat{\boldsymbol{n}}$で表現。ロドリゲスの式: $\boldsymbol{R}(\hat{\boldsymbol{n}},\theta) = \boldsymbol{I}+\sin\theta[\hat{\boldsymbol{n}}]_\times +(1-\cos\theta)[\hat{\boldsymbol{n}}]^2_\times$
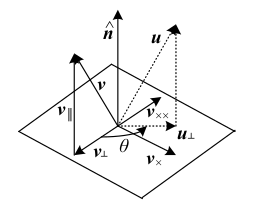
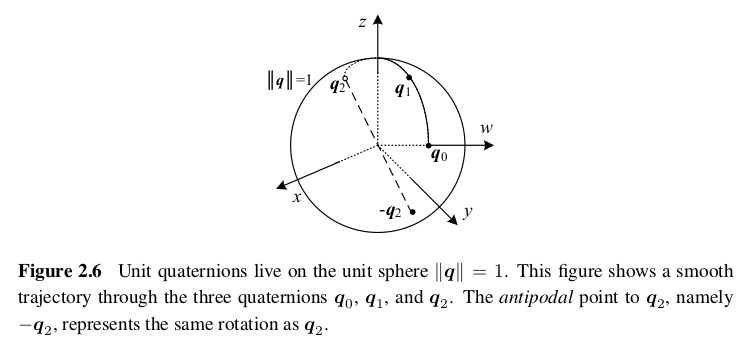
単位クォータニオン(単位四元数)
単位四元数は長さが1の4次元ベクトル、各要素は$\boldsymbol{q}=(q_x,q_y,q_z,q_w)$もしくは$\boldsymbol{q}=(x,y,z,w)$と表される。単位四元数による回転表現は一意的、かつ連続的。