オプティカルフロー(Optical Flow)

目的

このチュートリアルでは

  • オプティカルフローの概念と，Lucas-Kanade法を使ったオプティカルフローの計算方法を学ぶ．
  • 同画像中の特徴点の追跡のために cv2.calcOpticalFlowPyrLK() 関数などを使う．

オプティカルフロー(Optical Flow)

オプティカルフローとは、物体やカメラの動きによって生じる隣接フレーム間の物体の動きの見え方のパターンのことである．それぞれのベクトルが、1フレーム目から2フレーム目への変位ベクトルを表す2次元ベクトル場で表現される．下の画像(画像引用: Wikipedia article on Optical Flow) を見てみよう．

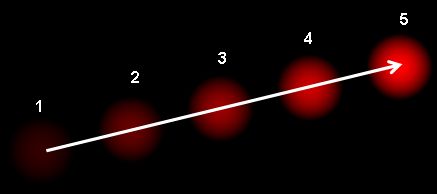
Optical Flow


この画像は連続する5フレーム中でのボールの動きを表す画像である．矢印は変位ベクトルを表す．オプティカルフローは下に示す様々なアプリケーションで使われる:

  • Structure from Motion(動きを基にした3次元復元)
  • 動画像の圧縮
  • 動画像の安定化(Stabilization)

オプティカルフローでは幾つかの仮定がある:

  1. 連続フレーム間で物体の画像上の明るさは変わらない．
  2. 隣接する画素は似たような動きをする．

1枚目の画像中の画素 $I(x,y,t)$ を考える($t$は時間軸方向を表す次元)．時刻$ dt $後に撮影された画像の中で $(dx,dy) $の距離を移動したとする．この二つの画素は同じものを見ていて，かつ明るさは変わらないと仮定したので，以下の関係が成り立つ．

$I(x,y,t) = I(x+dx, y+dy, t+dt)$

定式の右辺をテイラー展開し，共通する項を取り除き dt で割ると以下の式を得る:

$f_x u + f_y v + f_t = 0 $

ここで:

$\displaystyle f_x = \frac{\partial f}{\partial x} \; ; \; f_y = \frac{\partial f}{\partial x}$
$\displaystyle u = \frac{dx}{dt} \; ; \; v = \frac{dy}{dt}$

この式をオプティカル・フロー方程式(Optical Flow equation)と呼ぶ。画像の勾配を表す式である $f_x$ と$f_y$ が計算でき、同様に時間軸方向の勾配 $f_t$ も計算できる．しかし， $(u,v)$ が未知であり、未知数が2つあるのに式が一つしかないため，この問題を解くことができない。そこでこの問題を解くために色々な手法が提案されてきた．Lucas-Kanade法はその一つである．

Lucas-Kanade法

先ほど全ての隣接画素は似たような動きをすると仮定した．Lucas-Kanade法は，ある点に対してその点を含む周囲の3x3のパッチに含まれる9画素が同じ動きをしていると仮定し，この9画素の情報を基に ($f_x, f_y, f_t$) を計算する．これで二つの未知数に対して式が9本あるので，優決定系(over-determined)の線型方程式が得られる．よりよい解法がは線型フィッティングによって得られる．2個の変数に対し式を2つ持つ最終的な解法を以下に示す．

$\displaystyle \begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} \sum_{i}{f_{x_i}}^2 & \sum_{i}{f_{x_i} f_{y_i} } \\ \sum_{i}{f_{x_i} f_{y_i}} & \sum_{i}{f_{y_i}}^2 \end{bmatrix}^{-1} \begin{bmatrix}

- \sum_{i}{f_{x_i} f_{t_i}} \\
- \sum_{i}{f_{y_i} f_{t_i}}

\end{bmatrix} $ </CENTER>
(右辺の逆行列がHarrisのコーナー検出器に似ている点を確認しよう．このことはコーナーが物体追跡にとって適した点であることを意味する．)

使用者の観点から見ると、このアイディアは単純で，追跡のために点を幾つか指定し，これらの点のオプティカルフローを受け取るものである．しかし，ここで問題が発生する．これまでは小さい運動を扱っていたが，大きな動きに対しても問題なく追跡できるのだろうか．そこで画像ピラミッドを用いる．ピラミッドのスケールをアップすると，小さな動きが消され、大きな動きが小さな動きとして観測される．Lukas-Kanade法をこの解像度で適用することで，そのスケールでのオプティカルフローが得られる．

OpenCVにおけるLucas-Kanade法

OpenCVは上記の全ての処理を行う cv2.calcOpticalFlowPyrLK()という関数を用意している．ここでは同画像中の複数の点を追跡するアプリケーションを作成する．追跡する点を決めるために cv2.goodFeaturesToTrack(image, maxCorners, qualityLevel, minDistance{ corners{, mask{, blockSize{, useHarrisDetector{ k}}}}}) 関数を使う．1枚目の画像を撮影し，Shi-Tomasiのコーナーを検出する．それ以降，Lucas-Kanade法を使ってこれらの点を繰り返し追跡する．関数 cv2.calcOpticalFlowPyrLK(prevImg, nextImg, prevPts, nextPts{, status{, err{, winSize{, maxLeve{, criteria{, flags{, minEigThreshold}}}}}}}) を使う場合，前フレーム(prevImg)，前フレームでの点の位置(prevPts)，現フレーム(nextImg)、現フレームでの点の位置(nextPts)を指定する．戻り値は次のフレームでの点の位置と状態である．状態は、次の画像中で点が見つかれば1，そうでなければ0という値である．新しく検出した点を更に次のフレームでの入力に使用し，この処理を繰り返し行う．コードは以下のようになる:(使用した画像)

In [19]:
import numpy as np
import cv2

cap = cv2.VideoCapture('test.avi')

# params for ShiTomasi corner detection
feature_params = dict( maxCorners = 100,
                       qualityLevel = 0.3,
                       minDistance = 7,
                       blockSize = 7 )

# Parameters for lucas kanade optical flow
lk_params = dict( winSize  = (15,15),
                  maxLevel = 2,
                  criteria = (cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 0.03))

# Create some random colors
color = np.random.randint(0,255,(100,3))

# Take first frame and find corners in it
ret, old_frame = cap.read()
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)
p0 = cv2.goodFeaturesToTrack(old_gray, mask = None, **feature_params)

# Create a mask image for drawing purposes
mask = np.zeros_like(old_frame)

while(1):
    ret,frame = cap.read()
    if (ret == False):
       break
    frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)

    # calculate optical flow
    p1, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)

    # Select good points
    good_new = p1[st==1]
    good_old = p0[st==1]

    # draw the tracks
    for i,(new,old) in enumerate(zip(good_new,good_old)):
        a,b = new.ravel()
        c,d = old.ravel()
        mask = cv2.line(mask, (a,b),(c,d), color[i].tolist(), 2)
        frame = cv2.circle(frame,(a,b),5,color[i].tolist(),-1)
    img = cv2.add(frame,mask)

    cv2.imshow('frame',img)
    k = cv2.waitKey(30) & 0xff
    if k == 27:
        break

    # Now update the previous frame and previous points
    old_gray = frame_gray.copy()
    p0 = good_new.reshape(-1,1,2)

cv2.destroyAllWindows()
for _ in range(5):
    cv2.waitKey(1)
cap.release()

(このコードでは次の特徴点の正確性は確認していない．つまり，画像中で特徴点が見えなくなったとしても，その点に似ている特徴点が次のフレームにあればオプティカルフローを計算してしまう可能性があるわけである．頑健な追跡を実現するためには，コーナー検出は特定の間隔で行われるべきである．OpenCVでは5フレーム毎に特徴点検出を行っている．また，オプティカルフローの逆方向への探索を行い、安定した追跡結果だけを選択している．サンプルファイル samples/python2/lk_track.py(ウェブカメラ使用) を確認すること)．

この結果は

OpenCVでの密なオプティカルフロー

Lucas-Kanade法が出力するオプティカルフローは疎な特徴である(上記のコードではShi-Tomasiアルゴリズムによって検出したコーナーである)．OpenCVは密なオプティカルフローを検出するためのアルゴリズムを別に用意している．画像中の全画素に対してオプティカルフローを計算する．Gunner Farnebackが2003年に発表した “Two-Frame Motion Estimation Based on Polynomial Expansion” で提案されたアルゴリズムに基づいている．

以下のサンプルはこのアルゴリズムを使って密なオプティカルフローを計算する．出力として，オプティカルフローベクトル $(u,v)$ を格納した2チャンネルの配列が返ってくる．オプティカルフローの強度と方向を計算し，カラーコード化した画像を下に示す．方向はHue成分，強度はValue成分によって表されている．以下のコードを見てみよう:

In [20]:
import cv2
import numpy as np
cap = cv2.VideoCapture("test.avi")

ret, frame1 = cap.read()
prvs = cv2.cvtColor(frame1,cv2.COLOR_BGR2GRAY)
hsv = np.zeros_like(frame1)
hsv[...,1] = 255

while(1):
    ret, frame2 = cap.read()
    next = cv2.cvtColor(frame2,cv2.COLOR_BGR2GRAY)

    flow = cv2.calcOpticalFlowFarneback(prvs,next, None, 0.5, 3, 15, 3, 5, 1.2, 0)

    mag, ang = cv2.cartToPolar(flow[...,0], flow[...,1])
    hsv[...,0] = ang*180/np.pi/2
    hsv[...,2] = cv2.normalize(mag,None,0,255,cv2.NORM_MINMAX)
    rgb = cv2.cvtColor(hsv,cv2.COLOR_HSV2BGR)

    cv2.imshow('frame2',rgb)
    k = cv2.waitKey(30) & 0xff
    if k == 27:
        break
    elif k == ord('s'):
        cv2.imwrite('opticalfb.png',frame2)
        cv2.imwrite('opticalhsv.png',rgb)
    prvs = next

cap.release()
cv2.destroyAllWindows()
for _ in range(5):
    cv2.waitKey(1)

この結果は以下：

OpenCVのサンプルの中には，更に発展的な内容もあるので，samples/python2/opt_flow.py を参照のこと．

補足資料

  1. Gunner Farneback (2003)“Two-Frame Motion Estimation Based on Polynomial Expansion” In Proceedings of the 13th Scandinavian conference on Image analysis. pp. 363--370.

課題

  1. OpenCVのサンプルコードの samples/python2/lk_track.pyを読み、内容を理解せよ．
  2. OpenCVのサンプルコードの samples/python2/opt_flow.pyを読み、内容を理解せよ．

参考

ffmpegを用いて(OpenCV3で扱える動画形式の)Motion JPEG形式のファイルに変換する

 ffmpeg -i small.avi -b 2000 -r 29.97 -s 640x480 -vcodec mjpeg -an test.avi