SIFT (Scale-Invariant Feature Transform, スケール不変の特徴変換)の紹介

目的

このチュートリアルでは

  • SIFTアルゴリズムの概念を学ぶ
  • SIFT「特徴点」(キーポイント)と「特徴量記述」の見つけ方を学ぶ.

理論

参考: 藤吉氏によるSIFTの紹介が分かりやすい

これまでの章で、Harrisの手法などのコーナー検出の方法を学んだ。これらの手法は回転不変であった。つまり、画像が回転していても、同じコーナーを見つけられる手法であった。画像が回転してもコーナーはコーナーのまま、というのは明らかである。しかし、スケール（拡大縮小）についてはどうであろうか。画像が拡大縮小されたら、コーナーはコーナーでなくなってしまわないだろうか。例えば下の画像を見てみよう。左の画像にある小さなウィンドゥの中のコーナーが右図のように拡大されている。ここで右図の画像を同じサイズのウィンドゥでつぎつぎ取り出して見ていくと、もはやコーナーはなくなっている。このことから明らかなように、Harrisの方法はスケール不変とはいえない。

Scale-Invariance

そこで ブリティッシュ・コロンビア大学の D.Loweが2004年に論文 Distinctive Image Features from Scale-Invariant Keypointsで新しいアルゴリズムを提案した。その名をスケール不変特徴変換(Scale Invariant Feature Transform, SIFT)といい、画像から特徴点（以後、「キーポイント」と呼ぶ)を抽出し、「特徴量記述」を計算するという手法である。(この論文は理解しやすく、SIFTについての文献のなかで最良のものである。ここではこの論文の短い内容紹介に留める)。

SIFTアルゴリズムは主に4つのステップからなる。これを一つ一つ見ていこう。

以下を理解するための復習:ラプラシアン、ガウシアン・フィルタ、ガウシアンピラミッド & オクターブ

1. スケール空間における極値検出

上の画像の例からわかるように、同じウィンドゥを用いていろいろなスケールでキーポイントを検出するのは無理である。小さなコーナーなら大丈夫でも、大きなコーナーの検出には大きなウィンドゥでないとダメであったりする。そのため、スケール空間フィルタリングが使われる。そこではいろいろな $\sigma$値に対しガウシアンフィルタで平滑化した後にラプラシアンフィルタを適用する(合わせてLoG (Laplacian of Gaussian) フィルタという)。このLoGフィルタは$\sigma$における変化からいろいろなサイズのしみ(blob)を検出するような働きをする. 要するに $\sigma$ はスケール・パラメータとして機能する。例えば上の画像では、小さな $\sigma$をもつガウシアン・カーネルは小さなコーナーに対して大きな値を与え、大きな$\sigma$ をもつガウシアン・カーネルは大きなコーナーに適合する。それゆえ、 我々はいろいろなスケールと空間にわたって局所的極値を見つけることができる、つまり $(x,y,\sigma)$値---場所 $(x,y)$ に $\sigma$ スケールでキーポイントの候補があることを意味するもの---のリストを得ることができるのである。

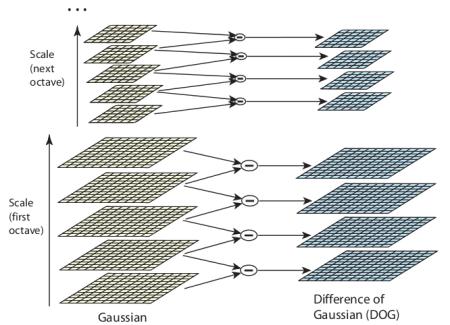
しかしこのLoGフィルタは計算コストが高い。そこでSIFTアルゴリズムではLoGの代わりにその近似としてガウシアンの差分(Difference of Gaussian, DoG)を用いる。DoGは異なる値の $\sigma$(それらを $\sigma$と $k\sigma$と表す)を用いて画像に対するガウシアンフィルタの値(平滑化)の差分から得られる。 この計算はガウシアン・ピラミッドにおける異なるオクターブに対して行われる。その過程を下の図で示す:

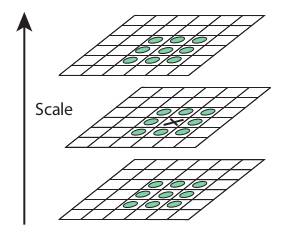
Difference of Gaussian このDoGが得られたら、次にスケールと空間にわたって画像の局所的極値を探索する。これを次のイラストで示そう。例えば画像の１ピクセル（下図のXマーク）をその近隣の８ピクセル、および前後のスケール（図では上下)それぞれ９ピクセルと比較する。 もしもそれが局所的極値であれば、キーポイント候補である。基本的に、キーポイントはそのスケールで一番よく表されるということを意味する。

Difference of Gaussian パラメータについては、Loweの論文で経験による値が与えられている。それによれば、オクターブの個数が4、スケールレベルの個数は５、最初の $\sigma=1.6, k=\sqrt{2}$ というのが最適値である。

2. キーポイントの局在化

先の処理によってキーポイントの候補の位置が決まると、より正確な結果を得るために、この候補を絞りこまなければならない。ここではスケール空間のテイラー展開により極値のより正確な位置を求め、この極値の大きさ(0〜1の値を取る)が閾値(論文では0.03)よりも小さいものは削除する。この閾値はOpenCVではコントラストによる閾値(contrastThreshold)と呼んでいる。

エッジのDoG値も高い値なので、エッジも削除しなければならない。このためHarrisのエッジ検出の方法と同様、$2\times 2$ のヘッセ行列 (H) を用いて主曲率を計算する。Harrisコーナー検出からの知見(「コーナー,エッジ,平坦領域の判別」の項を参照)から、エッジは２つの固有値に大きさの違いがある。そこで第１固有値を$\alpha$, 第２固有値を$\beta (\alpha > \beta)$とすると $\gamma = \alpha/\beta$ という固有値の比率を使う。

この比率がOpenCVで言うところのエッジ閾値(edgeThreshold) よりも大きければ、そのキーポイントはエッジとして削除される。論文ではこの閾値は 10 としている。

このようにして小さな極値とエッジを削除したので、残るはコーナー候補として有望なキーポイントだけである。

3. 向きの算出

今度は、画像の回転に不変性をもたせるため、それぞれのキーポイントの「向き(orientation)」を計算する。スケールに依存してキーポイントの位置の周りの点を取り出し、その領域における勾配の大きさと向きを計算する。36個のビンで360度すべての方向に対する勾配ヒストグラムが作られる(勾配の大きさと\sigma の値をキーポイントのスケールの1.5倍としたガウス関数で重みづけしている)。 このヒストグラムの最大値がそのキーポイントの向きとなる。ただし、その値から80%以上大きなピークがある場合、それも向きとして考える。この場合、同じ位置とスケールをもつキーポイントとなるが、最大値とは向きが異なる。こうすることでマッチングの安定性が得られる。

4. 特徴量記述子

次にキーポイント(特徴量)記述子を計算する。キーポイントの周辺16x16個の領域が取り出される。それを 4x4 のサイズに分け、16個の小ブロックを作る。それぞれの小ブロックに対し、それぞれ8個のビンをもつ勾配ヒストグラムを作る。これにより全部で 128個の値が得られることになる。それをベクトルで表現し、特徴量記述子とする。これに加えて、明るさの変化や回転などに対する頑健性を得るため、情報をいくつか加える。

5.　キーポイントのマッチング

２つの画像のそれぞれのキーポイントに対し、距離の近さにより同一性判定(異なる画像における特徴点の対応関係)を行う。しかし場合によっては(ノイズなどのため)、最も近い点ではなく2番めに近い点の方が対応点ということがある。そういう場合は、最も近い距離と２番めに近い距離の比を考える。もしもこの比が 0.8以上であれば、これらは採用されない。論文によれば、この方法で、90%の誤りを防げたとともに、間違って不採用となった対応点の割合は 5% であった。.

以上がSIFTアルゴリズムの内容である。より詳しく理解したい場合は、原論文を読むことを強くおすすめする。ひとつだけ忘れないこと。これは特許が取られている。だからこのアルゴリズムはOpenCVの「無料モジュールではなく」有料モジュールに入っているのである。

OpenCVのSIFT

さて、ここではOpenCVで利用可能な SIFT 関数について見ていこう。キーポイント検出からはじめ、それを図示してみよう。まず[cv2.xfeatures2d.SIFT_create({, nfeatures{, nOctaveLayers{, contrastThreshold, edgeThreshold{, sigma}}}})関数を用いてSIFTオブジェクトを作る。ここでドキュメントで説明されているいろいろなパラメタを付け与えることもできる:(使用する画像)

In [1]:
%matplotlib inline
import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('home.jpg')
gray= cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)

sift = cv2.xfeatures2d.SIFT_create()
kp = sift.detect(gray,None)

img=cv2.drawKeypoints(gray,kp,img)

# cv2.imwrite('sift_keypoints.jpg',img)
plt.imshow(img)
plt.show()

特徴量記述子を計算するには、OpenCVは２つの方法を提供している:

  1. キーポイントを計算している場合、 sift.compute()によってキーポイントから特徴量記述子を計算する。その例: kp,des = sift.compute(gray,kp)
  2. キーポイントを求めていない場合、sift.detectAndCompute()関数を用いて１ステップで直接キーポイントと特徴量記述子とを計算する。

ここでは２番目の方法を試す:

In [2]:
sift = cv2.xfeatures2d.SIFT_create()
kp, des = sift.detectAndCompute(gray,None)
In [4]:
print(len(kp))

889
In [6]:
print(des.shape)

(889, 128)

ここで kp はキーポイントのリストであり、desは「キーポイントの個数×128」という形状のNumpy配列である。

さて、これでキーポイントと特徴量記述子とを得られた。今度は、異なる画像でどのくらいキーポイントがマッチするかをみてみたい。これについては後続の章で扱うことにしよう。

補足資料

Lowe, D. (2004) Distinctive image features from scale-invariant keypoints. Int. Journal of Computer Vision. 60(2). pp.91-110．