K-Meansクラスタリングの理解¶

目的¶

このチュートリアルにより、K-Meansクラスタリングの概念や、その動作原理などを理解する．

理論¶

よく使われる例を使って理論を理解しよう．

Tシャツのサイズ問題¶

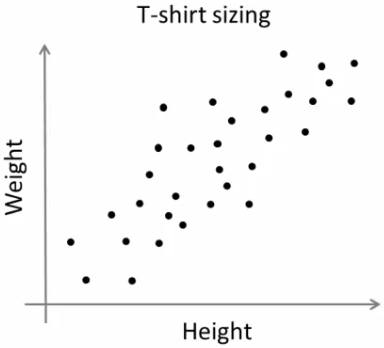
新しいTシャツのモデルを売り出そうとしている会社を想像してみよう．その会社では、あらゆるサイズの人々を満足させるよう、いろいろなサイズのモデルを製作すだろう．そこで、人々の身長と体重のデータを集め，下図のようなグラフを得たとしよう:

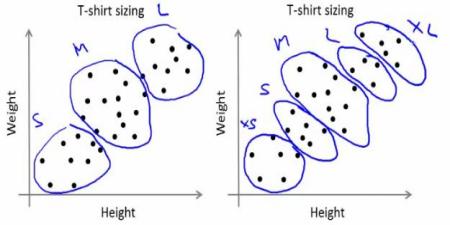
しかし実際には、会社はあらゆるサイズのTシャツを作ることはできない．その代わり，人をSmall, Medium, Largeの3種類に分割し，どの人にも合うようこの3つのモデルだけを作るであろう．このように人を3つにグループ分けすることは、k-meansクラスタリングによって可能であり、このアルゴリズムは、どの人も満足させるようなベストの3通りのサイズを決めることができる．もしもできない時には、3ではなくそれより多い(例えば5)グループに分割することになる．下の図をみてみよう:

動作原理¶

このアルゴリズムは繰り返し処理の一つである。図を使って少しずつ説明していこう．

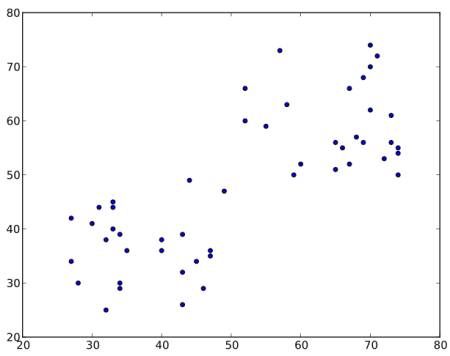
下図に示すようなデータを考えよう(今考えたTシャツのサイズ問題とみなしてもよい)．我々はこのデータを2つのグループに分ける(クラスタリングする)必要がある．

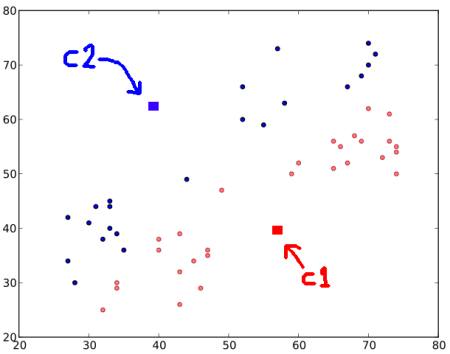
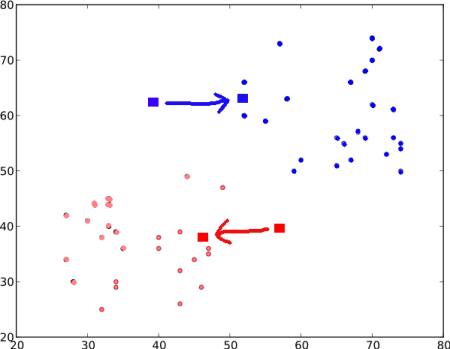
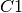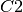ステップ 1: まずランダムに散布図の2個の座標 $C1$ と $C2$ を選び重心(centroid)(仮に)とする(データから2点を重心としてランダムに選択することもある)．

ステップ 2: この重心それぞれとデータとの距離を計算する．そして 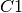$C1$ の方に近いデータは ‘0’ とラベル付けし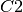， $C2$ の方に近いデータは ‘1’ とラベル付けする(もそも重心の個数が多ければ，さらに ‘2’,‘3’ とラベルを増やす)．

ここで、‘0’ とラベル付けされたデータはみな赤色で， ‘1’ とラベル付けされたデータはみな青色を塗ると，以下のような図が得られる．

ステップ 3: - 次にすべての赤点の座標の平均を計算し，その点を新しい重心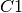 $C1$ とする．同様に、すべての青点の座標の平均は 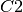$C2$ とする。このようにして重心の位置を更新する(ここに載せている画像は正確なデータではなく、あくまでもデモンストレーションである点に留意せよ)．

そして，新しく求めた重心を使って再びステップ 2の計算を行い、データすべてに‘0’ か ‘1’ のラベルを与える。

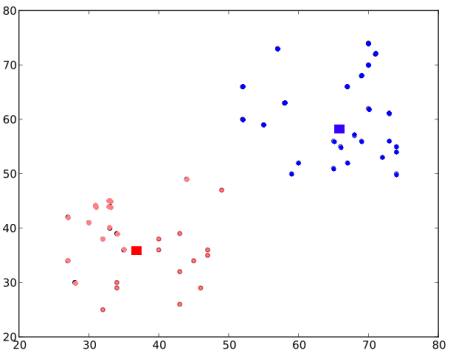
この結果が以下の図である:

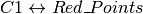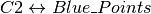重心の位置が更新されなくなる(つまり不動点に収束する)まで ステップ 2 と ステップ 3 を繰り返す (ただし、「最大繰り返し回数」や「特定の精度」が終了条件として与えられている場合は、収束しなくとも停止することがある)．: これらの重心は、そのグループのデータとの距離の総和が最小となる点となる．もっと簡単にいえば $C1 \leftrightarrow Red\_Points$ の距離と $C2 \leftrightarrow Blue\_Points$ の距離の和が最小となる点である．