k近傍法(k-Nearest Neighbor)の理解¶
目的¶
このチュートリアルではk近傍法(kNN)アルゴリズムの概念を学ぶ．
理論¶
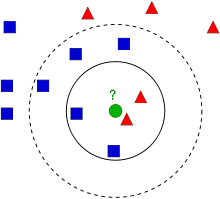
k近傍法(k-Nearest Neighbor, kNN)は教師あり学習のための分類アルゴリズムの中で最も単純なアルゴリズムの一つである．k近傍法のアイディアは特徴空間中でテストデータに最も似ているデータを探すという所である．下の図を用いて説明する．
この絵には青い四角と赤い三角という２つのグループがある ．それぞれのグループを クラス(class) と呼ぶ． クラスに属すメンバー(データ)は、特徴空間(feature space) と呼ぶ地図上に示されている (特徴空間は全てのデータが写像された空間とみなせる．例えば2次元座標空間を考えてみよう．それぞれのデータはx座標と y座標という２つの特徴を持つ．この2次元座標空間によってこれらのデータを表すことができる．特徴が3つなら3次元空間が必要になる．では特徴がN個ならどうだろうか。当然N次元空間が必要になる．このN次元空間こそがN個の特徴をもつものに対する特徴空間である．したがって、上の絵は２つの特徴を持つ2次元空間とみなせるのである) ．
ここで，緑の円で表される新しいデータが得られたとしよう．このデータを青四角か赤三角のどちらかのグループに所属させばければならないとする．この過程を 分類(classification) と呼ぶ．具体的にどうすれば分類できるのだろうか?ここではk近傍法を使って分類をしてみよう．
一つのやり方は、新しいデータに最も近いデータを調べることである．絵を見ると，新しいデータに一番近いデータは赤三角である．従って，この新しいデータを赤三角のグループに追加する．この方法は最近傍法(Nearest Neighbour) と呼ばれている。最も近い距離にあるデータだけに基づく分類だからである．
しかし，この方法には問題がある．確かに赤三角のデータが緑円に最も近かったが，周囲のデータには青四角のデータが多数あったならどうだろうか?そのような状況なら，赤三角のグループより青四角のグループに属している可能性が高くなる．つまり，最も近いデータだけを見るのは不十分である．その代わり、最も近い k 個のデータを見ることにする．その中で多数を占めているデータのグループに，新しいデータを分類すればよい．例として、上の絵において k=3、つまり最も近い3個のデータを考えて分類してみよう．緑円の近くには赤が2つ，青が1つ(2つの青四角が等距離に存在するが，k=3と設定しているので、その内の1つだけを採用する)ある．そこで，k=3では緑円は赤三角グループに加えられることになる．では k=7ならどうだろうか? この時は青四角グループのデータが5個，赤三角グループのデータが2個なので、今度は緑円は青四角グループに加えられることになる．このように、この方法はkの値によって結果が変わる可能性がある．さらに面白いことに k = 4 としたら、どうだろうか?この場合は赤三角のグループも青四角グループも緑円の近傍にそれぞれ2個ずつあり、多数決ができない．つまりこのことから，kの値は奇数のほうが良いことが分かる．この方法はkの値に依存する分類法であるため，この方法は k近傍法(k-Nearest Neighbour) と呼ばれる．
今述べたように、k近傍法ではk個の近傍点(データ)を考慮しているが，すべてのデータを同等に扱っている。これは正しいのだろうか？例えば， k=4 のケースをもう一度考えてみよう．結果は引き分けと述べたが，よく見ると赤三角グループの方が青四角のグループよりも緑円データに近い位置にある．このことを考慮すると，緑円は赤三角グループに加える方がよさそうである．これを次のように数学的に表してみよう。それぞれのデータに対し，新しいデータとの距離に応じた「重み」を与える：新しいデータに近ければ大きな重みを，遠ければ小さな重みを与える．そしてそれぞれのクラスごとに、新データに近いデータの重みの総和を求める．そこで最大の重みが得られたクラスに新データを所属させればよい．この方法を 変形k近傍法(modified kNN) という．
ここで重要な点は何だろうか?
- すべてのデータの地図上の位置が必要である。なぜなら新データに近い点を見つけるには、新データと他のすべてのデータとの距離を求める必要があるからである．もしデータもグループも大量にあるのなら，大量のメモリを消費し，計算時間も多くかかるだろう．
- 学習や準備にかける時間はほとんど不要である．
それではOpenCVにおけるk近傍法をみていこう．
OpenCVにおけるk近傍法¶
ここでは今の例と同じく，2つのグループ(クラス)を使った簡単な例を扱う．次のチュートリアルでは、これよりも良い例を扱う．
ここでは赤のグループを Class-0 (0と書く)，青のグループを Class-1 (1と書く)とする．25個のデータ(学習データ)を作り，それぞれのデータに対しClass-0かClass-1のどちらかのラベルを与える(グループ分け)．この作業にはNumpyの乱数生成器を使おう．
次にMatplotlibを用いて、生成したデータをプロットする．赤のグループは赤の三角形，青のグループは青の四角形としてプロットしよう．(コード)
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 25個の学習データに対する(x,y)座標からなる特徴集合
trainData = np.random.randint(0,100,(25,2)).astype(np.float32)
# 学習データそれぞれに赤と青のクラスに相当する0と1をラベル付する
responses = np.random.randint(0,2,(25,1)).astype(np.float32)
# 赤のクラスのデータをプロット
red = trainData[responses.ravel()==0]
plt.scatter(red[:,0],red[:,1],80,'r','^')
# 青のクラスのデータをプロット
blue = trainData[responses.ravel()==1]
plt.scatter(blue[:,0],blue[:,1],80,'b','s')
plt.show()
このチュートリアルで最初に見せた絵と同じようなプロットが表示されているはずである．もっとも乱数生成器を使っているため，コードを実行する度に異なるデータが得られる．
次にk近傍法のオブジェクトを初期化し， k近傍を学習するために trainData(学習データ) と responses(応答値) を与える(検索木を構築する)．
そして、新しいデータを一つ作り，OpenCVのk近傍法を使ってどのクラスに属するデータか、分類する．k近傍法を使う前に，テストデータ(新しく作成したデータ)について知っておく必要がある．データは，サイズが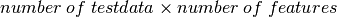 
の浮動小数型の配列でなければならない．次の処理は新しいデータのk近傍点の検索である．ここでkの値(何個の近傍点を考慮するか)を指定できる．最近傍法(Nearest Neighbour)を使う場合は k=1 と設定する．k近傍法を使うと，戻り値として:
- このチュートリアルで学んだk近傍法により求めたテストデータのラベル(クラス)．
- k近傍点のラベル．
- テストデータとk近傍点との距離．
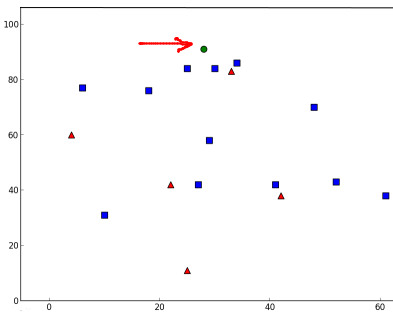
それではどのようにk近傍法が機能するか見てみよう．テストデータを緑色の円として表示する．(コード)
newcomer = np.random.randint(0,100,(1,2)).astype(np.float32)
plt.scatter(newcomer[:,0],newcomer[:,1],80,'g','o')
knn = cv2.KNearest()
knn.train(trainData,responses)
ret, results, neighbours ,dist = knn.find_nearest(newcomer, 3)
print("result: ", results)
print("neighbours: ", neighbours)
print("distance: ", dist)
plt.show()
以下のような結果が得られた:
result: [[ 1.]]
neighbours: [[ 1. 1. 1.]]
distance: [[ 53. 58. 61.]]
この結果においては，テストデータの3個の近傍点は全て青グループに属していた．従って、テストデータには青クラスのラベルが与えられた．これは下のプロットから明らかであろう:
もしも大量のデータがある場合は，データを配列の形で渡せる．なお、これに応じて処理結果も配列として出力される．(コード)
# 10 個のテストデータ
newcomers = np.random.randint(0,100,(10,2)).astype(np.float32)
ret, results,neighbours,dist = knn.find_nearest(newcomers, 3)
# 結果も10個のラベルからなる配列.
補足資料¶
- NPTEL notes on Pattern Recognition, Chapter 11
- Scikit-learn: Pythonの機械学習パッケージの最近傍法の項
