この二進木の場合、「20 10 15 4 7 11 6 1 3 5 2」は今の条件を満たしていますので、(二進)木のなぞりになっています。 ただ、(二進)木をなぞる方法は一通りではありません。たとえば「1 3 5 2 4 7 11 6 10 15 20」も条件を満たしているので、この(二進)木のなぞりといえます。
今回の学習項目です。
再帰呼び出しとは、関数の中で自分自身を呼び出すことであるということを 前の課題で述べました。 そこでは再帰のプログラムを理解して使いこなせることの重要性を強調しました。
ここはその復習にあたります。 とはいっても、同じことを繰り返しても面白みに欠けるので、 二進木のなぞりを例にとり、再帰呼び出しを学びます。
再帰呼び出しの特長は、「ある種の手続きを完結に表現できる--- したがって理解しやすくなる」ことにあります。これは特に、 その手続が扱う問題やデータ自体が再帰的な場合に有効です。
ここで、「 (二進)木のなぞり」とは
木の頂点のラベルをすべて、かつ重複なしに表示する(取り出す)
ことを意味します。ただし、ここで考える木の頂点はラベルを持つものとします。
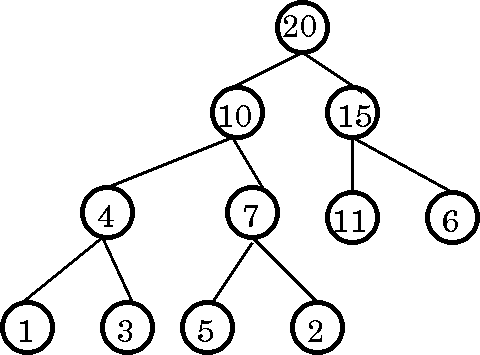
右図にあげる二進木をその例として考えましょう。

この二進木の場合、「20 10 15 4 7 11 6 1 3 5 2」は今の条件を満たしていますので、(二進)木のなぞりになっています。
ただ、(二進)木をなぞる方法は一通りではありません。たとえば「1 3 5 2 4 7 11 6 10 15 20」も条件を満たしているので、この(二進)木のなぞりといえます。
ここでは(二進)木をなぞる方法を考えます。そこで活躍するのが再帰関数です。
二進木は次のような部品から構成されています: 根、左の部分木、右の部分木。 ここで「部分木」というのは、木の一部とはなっているけれども、形は木と変わらないもの、を意味します。先の図で説明します。根と10のラベルをもつ頂点に注目してください。この2つの頂点を結ぶ枝を削除したとします。すると、ラベル10を根とする木が見えてくるでしょう。これが元の木に対する「(左の)部分木」です。同様に、根と15のラベルを持つ頂点との間の枝を削除して得られるラベル15を根とする木を、元の木に対する「(右の)部分木」と呼びます。 このように、どの二進木も、根、左の部分木、そして右の部分木に分割できます。
このように考えると、二進木は「再帰的な構造」を持つことが理解できるでしょう。
つまり、「二進木は、根、左の部分木(これは二進木)、そして右の部分木(これも二進木)から構成される」。
すると二進木をなぞる関数を
def traverse(tree)
if tree == nil # treeが木でない場合, 空配列を返す
return []
else
ans = traverse(treeの左部分木) + [treeの根のラベル] + traverse(treeの右部分木)
return ans
end # if
end # def
今の例にあげたtraverseでは、まず左の部分木の頂点のラベルを取り出し、 次に根の頂点のラベルを取り出し、最後に右の部分木の頂点のラベルを取り出す、 という「木のなぞり」方法であった。これを「中間順のなぞり」(inorder)という。 なぜなら、根のラベルを取り出すのが、「左と右の中間」だからである。
それに対し、(a)まず根のラベルを取り出してから左の部分木のラベルを取り出し、 次に右の部分木を取り出すという方法や、 (b)左の部分木と右の部分木のラベルを取り出してから最後に根のラベルを取り出すという方法が考えられる。 (a)を「先行順」(preorder)の木のなぞり、(b)を「後行順」(postorder)の木のなぞりと呼ぶ。
(a)、(b)それぞれの方法をtraverse関数にならってプログラムを書き、すべての頂点がもれなくしかも重複なく表示されることを確かめなさい。
ただし、それぞれの関数の名前をpreorderとpostorderとする。
注意: 実際に2進木をどのように表すかは(配列を用いて表すヒープを除いては)まだちゃんとはやっていません。これについては6月15日の課題で学びます。ですから、
ここで書くべきプログラムとは、上のtraverseの書き方にならったものとします。
(したがって、実際にRubyで走らせることはできません。「確かめよ」というのは、
自分の頭を使って、という意味です)
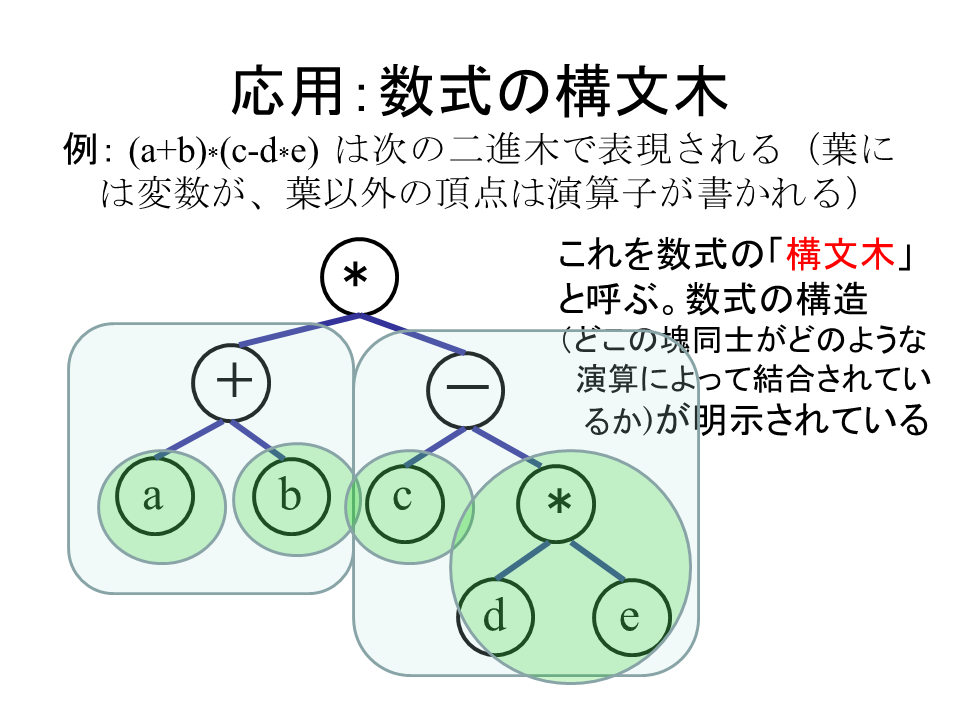
右図は (a+b)*(c-d*e) の数式を表現した二進木(数式の構文木という)である。
これにならって 12*3+(45 - 67)/8 という数式の構文木を書け。
課題1-2で書いた二進木を、(a)先行順、(b)中間順、(c)後行順でそれぞれなぞったときに何が表示されるかを書け。ちなみに先行順でなぞった時は「ポーランド式」、 後行順でなぞったときは「逆ポーランド式」の数式という。どちらも括弧なしで数式の構造を表すことができる方式である。