解説 6月14日A

今回の学習項目です。

• キュー
• Rubyによるキューの実現

キュー(Queue)

キューとは次の条件を満たすデータ構造です:

• 新しい情報を追加できる
• 古い情報の一つを取り出す。そのときには、最も古いものから順に取り出します。なお、取り出されたデータは削除されます。

キューは、追加と取り出し方法が制限された｢リスト構造」とみることもできます。

キューについて学ぶことは次の3点です。

1. どのようなデータ構造によってキューが実現できるか。
2. キューに固有な操作にはどのようなものがあるか。
3. キューを用いた応用にはどのようなものがあるか。

キューの実現方法

キューに固有な操作

• エンキュー(enqueue)：引数を1個とります。キューにその引数を新たなデータとして記憶します。
• デキュー (dequeue) ：引数は取りません。キューにおいてデータを取出します。取り出されたデータはキューから取り除かれます。

キューを用いた応用

一つの例は、優先度付きプロセスの処理（優先度付きキュー）です。 これは、例えて言えば、「窓口に並んだ列でも払ったお金によって並ぶ順番を変えられる」、というようなシステムです。

また人工知能で探索アルゴリズムとして有名なA*アルゴリズムもキューの応用とみなせます。将棋やオセロのようなゲームにおいて、現在の盤面から可能な「手」によってどのような盤面が生じるかを求め、それらを評価して、次の盤面(手）を選ぶという場合に用いられる方式です。 これは自分の手だけではなく相手の手によって盤面が変化し、しかもその評価が動的に(ダイナミックに）変わる、という性質があります。これは実質的には優先度付きプロセスの処理とほぼ同じものといえます。

キューをRubyのクラスとして定義してみましょう。初めの試みとして以下のように定義することを考えます。

class Queue
   def initialize()
       @data = []   # データの記憶用の配列
       @head = 0    # 先頭のデータの位置
       @tail = -1   # 最後尾のデータの位置
       @max = 10    # 記録できるデータの最大個数
       @number = 0  # 記録されているデータの個数
   end # initialize
   def enqueue(x)
       @tail += 1
       @number += 1
       @data[@tail] = x
   end  # def of enqueue
   def dequeue
       ans = @data[@head]  
       @head += 1
       @number -= 1
       return ans
   end  # def of dequeue
   def show  # キューの内容の表示
       return @data[@head..@tail]
   end # def of show
end # class

enqueueとdequeueのメソッドはそれぞれキューに要素を付け加える操作と、キューからデータを取り出す操作です。それぞれのメソッドを実行すると headとtailの値(それにnumberの値)が変化することに注意しましょう(もちろんdataの値も変わります)。 最後にshowはキューの状態を表示するためのもので、配列として要素が表示されます。

Rubyによる実現(2): 配列を効率よく使う

Rubyによる実現(その1)では、教科書の64ページ、 および図6.5(a)-(c)に書かれた方法で、配列を用いてキューを表現していた。 しかしこれでは教科書に書いてあるように、キューに新しいデータを格納したり取り出したりしているうちに、 headの値もtailの値も大きくなる一方なので、実際にキューに記憶されているデータは小さなものであっても、そのデータを記憶するために用意された配列は大きいままである。これはキューからは取り除かれているはずのデータが配列に残ったままであることが原因である。

そこでこのような無駄をなくすために、配列の大きさはあまり大きくしないようにし、 headやtailの値を工夫することでメモリの無駄が少ないキューを実現することを考えよう。

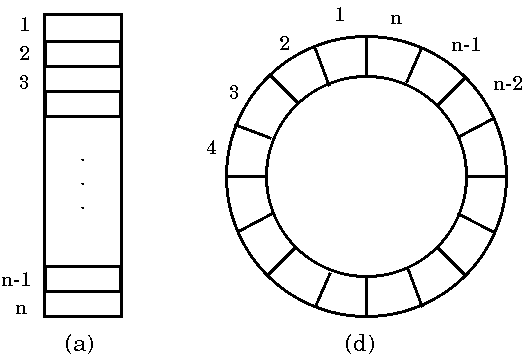
そのための方法として、教科書図6.5のように配列を環状のものと考えてみよう。 とは言っても、環状の配列、というものは存在しない。ここでは図6.5(a)に書かれたような(直線上に要素を並べた)配列を図6.5(d)のように見かけ上円のように並べるようにする、ということである。

ここで配列の大きさを固定しておく。仮にそれをnとする(nの値としては50や100を考える)。また、ここでは(話を簡単にするため)配列のインデックスは1から始まるものとする。 だから配列の要素のインデックスがとりうる値の範囲は、1, 2, ..., nとなる。

そして、headやtailの値がnを超えた場合、たとえばn+1やn+2のような場合には、 1や2のような値を与えるようにするのである。 具体的には、このような工夫をしなかった場合の配列のインデックスをx、 円環状の配列のインデックスをyとすると(ここで%は剰余を求める演算)

   y = (x-1)%n + 1

class Queue
   def initialize(n) # 記録できるデータの最大個数を引数とする
       @data = [nil]   # データの記憶用の配列。0番目の要素はダミー
       @head = 1    # 先頭のデータの位置
       @tail = 0   # 最後尾のデータの位置
       @max = n    # 記録できるデータの最大個数
       @number = 0  # 記録されているデータの個数
   end # initialize
   def convert(x)  # 変換のための関数
      y = (x-1) % @max + 1
      return y
   end  # def of convert
   def enqueue(item)
       if (@number < @max) # データの追加が可能なら        
          @number += 1
          # @tailを適切な値に設定するコードを書く(convertを使うこと)
          @data[@tail] = item
       else
          STDERR.print "Queue is empty\n" # warning message
       end # if        
   end  # def of enqueue
   def dequeue
       if (@number > 0)  # キューに要素があるなら        
          # @numberと@headを適切な値に設定し
	  # (convertを使うこと)
          # 適切な返り値を返すコードを書く
       else
          STDERR.print "Queue is empty\n" # warning message
       end # if
   end  # def of dequeue
   def empty  # キューが空ならtrue、そうでなければflaseを返す
       if (@number > 0)  # キューに要素があるか
           return false
       else
           return true
       end # if
   end # def of empty
   def show  # キューの内容の表示
       lst = []    # 改変されていることに注意
       for i in 0...@number
         lst << @data[convert(@head+i)]
       end # for
       return lst
   end # def of show
end # class

「アルゴリズムとデータ構造」のホームに戻る