今回の学習項目です。
教科書の2.2節の内容としては以下が重要です。
木構造は、おそらく離散数学などで学んだ概念だと思います。 この木構造は、アルゴリズムの設計でとても重要な役割を果たしています。 ここでは木構造のことを「根つき木」と呼んでいますが、単に「木」と呼んでもよいものです。
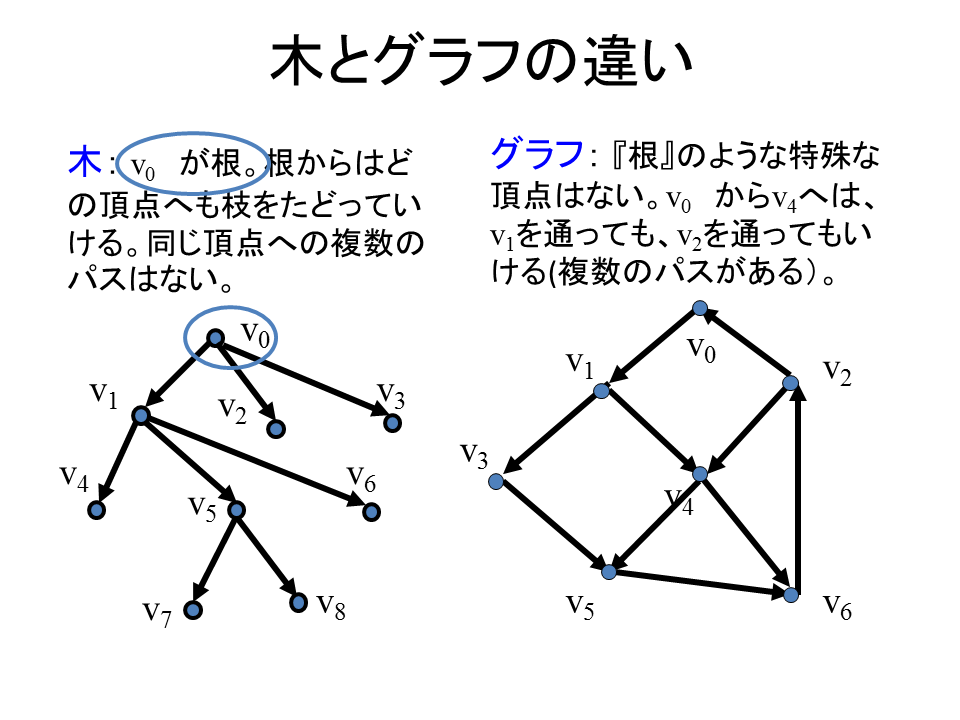
(根つき)木とは、図2.8に示されるような、特殊なグラフです。 ここで、グラフとは、頂点(「ノード」ともいう)と、頂点と頂点を結ぶ辺(「枝」ともいう)とから構成されているものです。 ただ、辺は頂点をその端に持たなければならない(ただし、同じ頂点であってもよい)という制約があります。なお、頂点にはそういう制約はありません。辺によって結ばれていない頂点があっても構いません。そのようなものがグラフです。
木は「根」と呼ばれる特別な頂点を持ち、すべての頂点が辺で結ばれるという特殊なグラフです。さらに、根からはいくつかの辺を経由してどの頂点にもたどっていけることと、さらにそのような根から頂点へのたどり方は必ず一通りに限ること(つまり、たどる方法が複数通りはないこと)という制限があります。
こういうとややこしそうですが、図2.8を上下逆さにしてみてください。 こうすれば「根」が図の下になります。そして本当の木のように(もしくは草のように)見えませんか?根から上へ上へと枝が伸びているようにみえませんか? これが「木」と呼ばれる理由です。このイメージをもっていれば、どんなグラフでも木か、そうでないかは容易に判定できます。
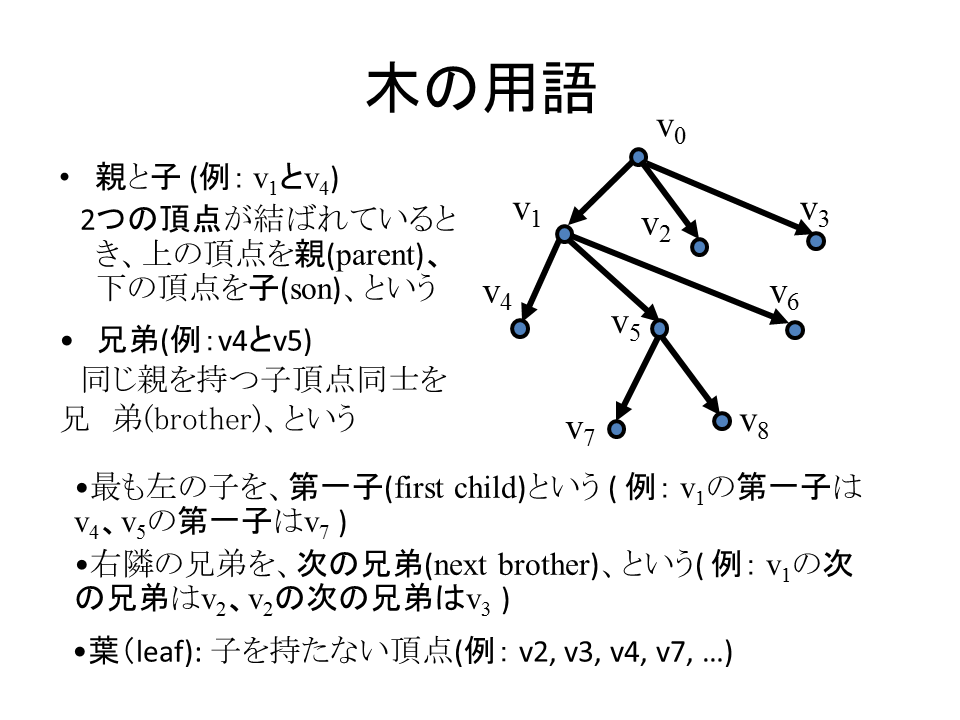
図2.8をもとに説明します。この図では根が一番上にあります。 そして他の頂点はその根の下にあります。これを家系図にたとえてみます。 根がご先祖様です。根の下にあり、根から辺一本で結ばれている頂点は、いわば根の「子」です。逆に言えば、これらの頂点からみると根は「親」にあたります。
図2.8において根の「子」に名前をつけてみます。左から順にv1, v2, v3とします。 (ここでvという記号をつかったのは、頂点の英語名から来ています。さて、頂点は英語では何と呼ばれているでしょう?) すると、v1, v2, v3は同じ親をもつ子ですから、これらは「兄弟」(「姉妹」ともいう)という関係にあります。
なお、v1にもv2にもv3にも子の頂点がいます。例えばv1の子からみると根は「祖父(grandparent)」にあたります。逆に根から見るとv1の子は「孫(grandson)」にあたります。すぐわかるように、根以外のどの頂点にも「親」がただ一つ存在します。また「祖父」があるとすればこれもただ一つに限ります。
ここでの用語の最後に、「葉」(leaf)を紹介します。木は根から幹や枝が伸び、花や葉となります。木構造では「花」はありませんが、「葉」はあります。葉とは、子を持たない頂点のことをいいます。たとえ根であっても、子がない場合は「葉」と呼ばれます。根であって葉でもある、というのは不思議ですね。でも理論としてはこういうことも可能なのです。
このページの「木の用語」と書かれている図を見て、以下の問に答えなさい。
木の頂点が教科書21ページ目の図2.9のように表されているとします。 つまり、頂点は「リスト構造」の一つのセルとして表され、 そのセルには「親」「次の兄弟」「第1子」それぞれの頂点(セル)へのポインタが書かれているのです。 ただし、「親」など該当する頂点がない場合は nilが値となっているとします。
教科書によれば、頂点vの子をすべて列挙するには次の手続きをとればよいとあります。
x <- FirstChild[v]
while x != nil do
report x and x <- NextBrother[x]
これにならって、頂点vの祖先をすべて列挙する手続きを書きなさい。
[教科書に書かれた手続きの解説]
x <- FirstChild[v]は、頂点vの「第1子」頂点を取り出し、変数xの値とすることを意味しています。 ここで、頂点vの「第1子」頂点がない場合は、xの値はnilが入ります。
while x != nil doつまり、「第1子頂点がない」場合は、繰り返しが行われずに終了です。 繰り返される手続きは以下です:
report x and x <- NextBrother[x]
report xは変数x (つまり頂点が代入されている)が何かをreport(報告)するという命令です。
ここでは頂点のラベルが印刷表示 (ここではprintとしておきます) されると思ってください。
次のandは、その次の
x <- NextBrother[x]
命令が続けて実行されることを意味しています。これによって変数xには頂点xの「次の兄弟」頂点が値となります
(またもや、そういう頂点がなければnilが代入されます。
Rubyで書くとすれば以下のようにかけるでしょう (ここで、頂点を表すクラスが用意されてあり、vはそのインスタンスが代入されているとしています。 が、このままではもちろん動きません。あくまで感触をつかむためのもの、と思ってください)
x = v.firstChild
while x != nil
p x.label
x = x.nextBrother
end # while
x <- FirstChild[v]
while x != nil do
report x and x <- NextBrother[x]
ここでは「孫」の列挙が必要です。孫とは「子」の「子」を意味します。
3行目の「くり返し」されている命令を考えましょう。この時点ではxは元の頂点の「子」でしかありません。
さらにその「子」を取り出さなければなりません。そこで3行目を次のように変えてみましょう。
y <- FirstChild[x]
while y != nil do
report y and y <- NextBrother[y]
すると、何がreportされることになるでしょうか?
class Vertex # クラスの定義の始まり
def initialize(l, p = nil, b = nil, f = nil) # インスタンスを作るためのメソッド
@label = l # label(頂点のラベル)を表す「要素」を定義
@parent = p # parent(親)を表す「要素」を定義
@nextBrother = b # nextBrother(次の兄弟)を表す「要素」を定義
@firstChild = f # firstChild(第1子)を表す「要素」を定義
end # of def
attr_accessor :label,:parent, :firstChild, :nextBrother # インスタンス変数へのアクセスを可能にする
end # of Class
z = Vertex.new("v3",r)
y = Vertex.new("v2",r,z)
x = Vertex.new("v1",r,y)
r.firstChild = x
これらで表される木はどのようなものでしょうか、答えなさい。
a = r.firstChild
while a != nil
print a.label," "
a = a.nextBrother
end # while