課題1-1
右図は、二進木の例です。ここでv0, v1, ... は頂点のラベルを表しています。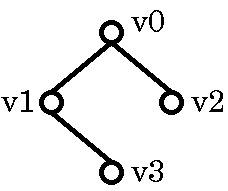
この木について、以下の問に答えなさい。
- これが二進木であることの根拠を述べなさい。
- 頂点v0の左の子頂点はどれか、答えなさい。
- 頂点v0の右の子頂点はどれか、答えなさい。
- 頂点v1の左の子頂点はどれか、答えなさい。
- 頂点v1の右の子頂点はどれか、答えなさい。
今回の学習項目です。
2進木は２分木とも呼ばれています。どちらも英語の binary tree の訳にあたります。
２進木とは、どの頂点においても、その子頂点の個数が２以下の木のことをいいます (別な言い方をすれば、子頂点の個数は「高々２個」）。 つまり、どの頂点に対しても、子頂点の数は0, 1, 2のいずれかです。
ここで、子頂点を「左の子」もしくは「右の子」という名前をつけて区別します。 そして図示する場合にも、親頂点に対して左の子は左に、右の子は右に書きます。 これはたとえ、子が一つしかなくても適用されます。そこで、２進木のどの頂点も、 子頂点は「ない（子頂点の数が０）」、「左の子だけがある（子頂点の数は１）」、 「右の子だけがある（子頂点の数は１）」、「左の子と右の子がいる（子頂点の数は２）」 のいずれかになります。
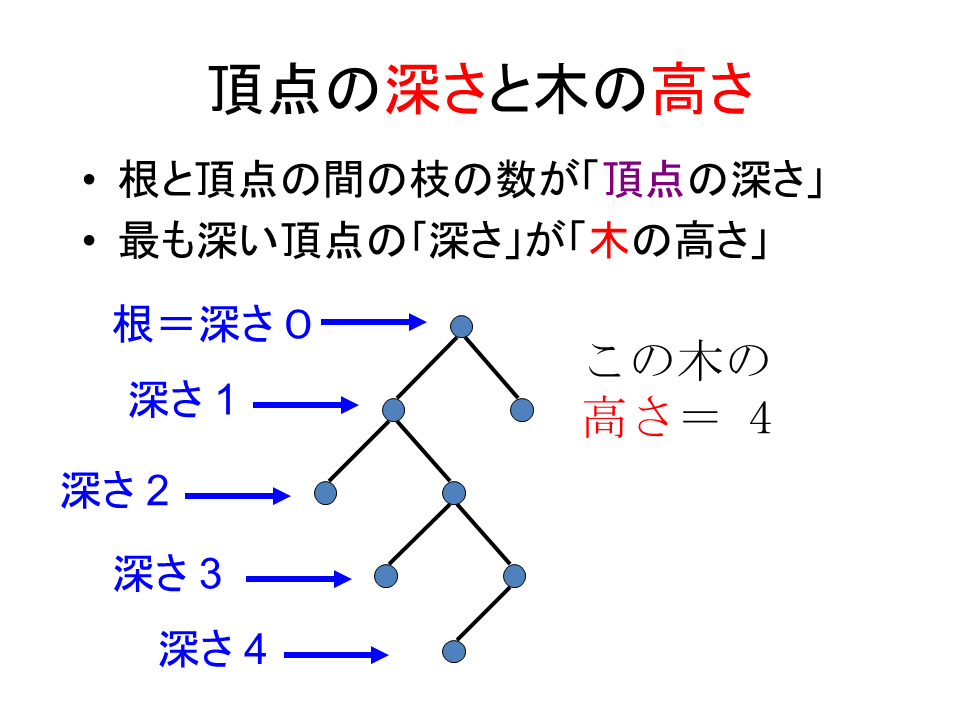「頂点の深さ(depth)」とは、根と頂点の間の枝の数のことです。
根そのものは(枝がないので)深さは0となります。すると根の子頂点は深さ1、孫頂点は深さ2となります。
どの木の頂点に対しても、このようにして深さが定義できます(根からどの頂点へも枝をたどっていけること、 またそのたどり方はひと通りに決まる、というのが「木」の性質であったことを思い出しましょう)。 すると、どの木においても、もっとも深い(言い換えれば、深さが最も大きい)頂点が存在します (複数個ある場合もあります)。その頂点の深さを「木の高さ(height)」 と言います。
これらの定義に基づいて、強平衡２進木が定義されます(p.27):
定義3.1 すべての不完全頂点の深さが高々１しか違わない２進木のことを 強平衡２進木という
これは次のようにも言い換えることができます: ２進木において、頂点の深さが最も小さい不完全頂点の深さと、 頂点の深さが最も大きな不完全頂点の深さの差が１以下ならば、強平衡２進木である
このような強平衡２進木の定義から、次の性質が導かれます(p.28)。 n個の頂点を持つ強平衡２進木の高さはO(logn)である
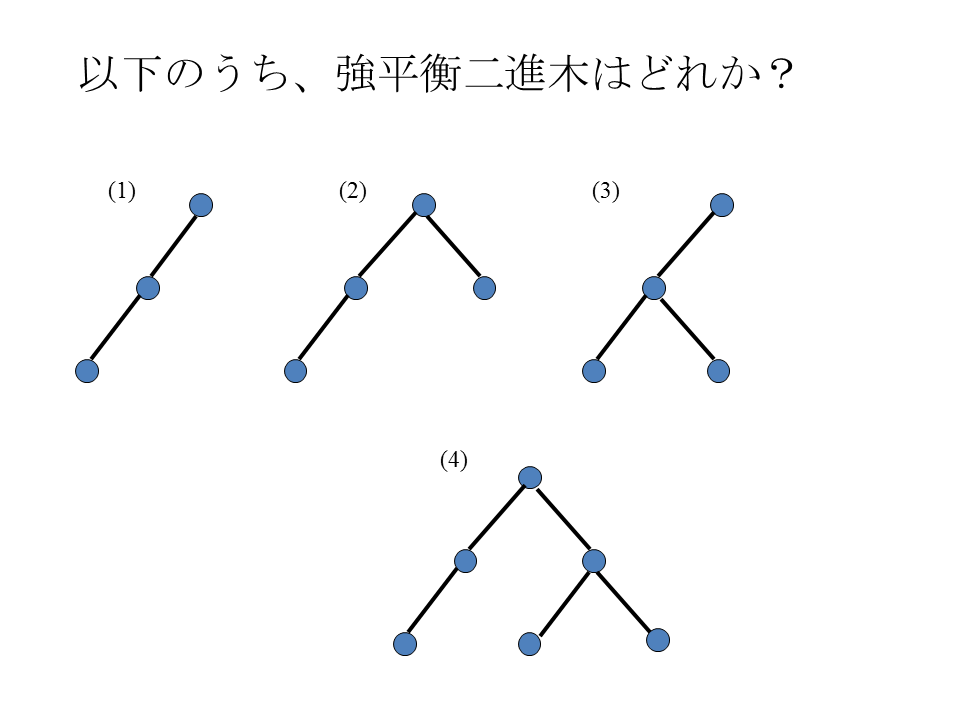
右図をみて、強平衡二進木であるものの番号を答えなさい。 また、強平衡二進木ではないものについて、なぜそれが強平衡二進木でないのかという理由を述べなさい。
教科書の説明を参考にして、強平衡二進木の性質としてあげた 「n個の頂点を持つ強平衡２進木の高さはO(logn)である」が成り立つ理由を自分の言葉で述べなさい。