6章のt検定は2つの群の平均値を比較しましたが、分散分析は3つ以上の群の平均値を比較します。
7.1, 7.2では1つの条件による母平均の違いの検定である一元配置の分散分析をとりあげました。
この講義では、教科書の第7章「分散分析」のうち、7.3~7.5の2つの条件の組み合わせによる「二元配置分散分析」をとりあげます。
例題:ミネラルウォーターの美味しさの評定に関する実験データ:
| 冷蔵庫 |
常温 |
| イカアン |
ボスビック |
ビビッテル |
イカアン |
ボスビック |
ビビッテル |
| 6 |
10 |
11 |
5 |
7 |
12 |
| 4 |
8 |
12 |
4 |
6 |
8 |
| 5 |
10 |
12 |
2 |
5 |
5 |
| 3 |
8 |
10 |
2 |
4 |
6 |
| 2 |
9 |
10 |
2 |
3 |
4 |
- 要因: 母平均に違いをもたらす原因
- 水準: ある要因の中に含まれる個々の条件
例題では;
| 要因 |
水準 |
| 温度の違い |
冷蔵、 常温 |
| 銘柄の違い |
イカアン、ボスビック、ビビッテル |
二元配置分散分析では、
主効果と交互作用効果という2種類の効果を考える
- 主効果: それぞれの要因ごとの効果 --- 一元配置分散分析のときに考えた効果と同じ
- 交互作用効果: 2つ以上の要因が組み合わされたときに生じる効果 ---2つの要因の効果の単純な足し算では説明できない効果
交互作用のある、なしに見られるデータの特徴: 以下ではinteraction.plotという、
交互作用効果を確認するための平均値のプロットを作成する関数を用いています:
| 交互作用のないデータ |
交互作用があるデータ |
パターンの例:
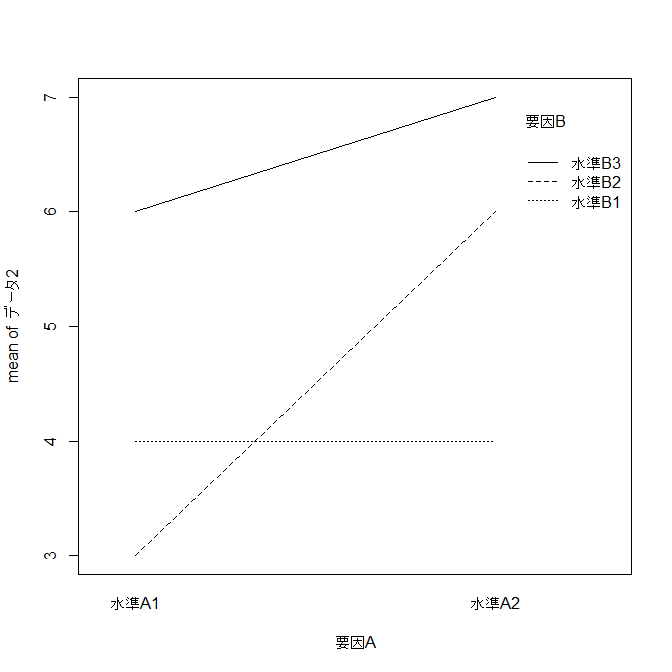
| | B1 | B2 | B3 |
| A1 | 4 | 3 | 6 |
| A2 | 6 | 5 | 8 |
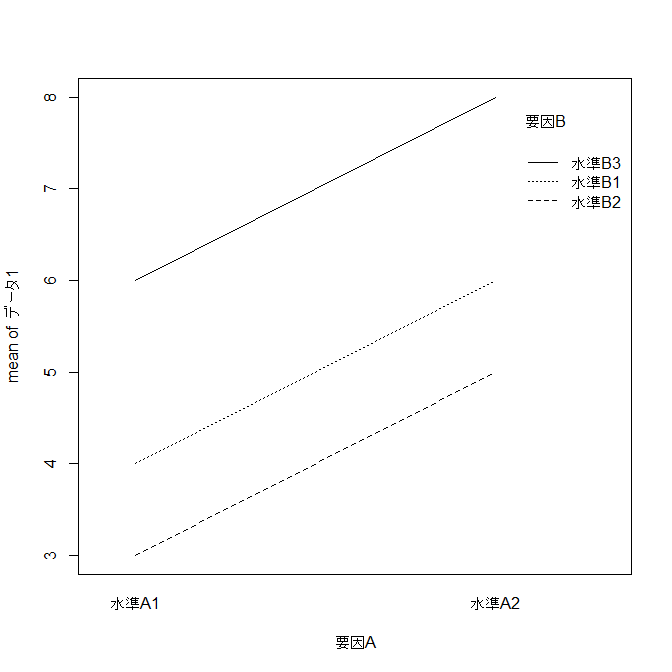
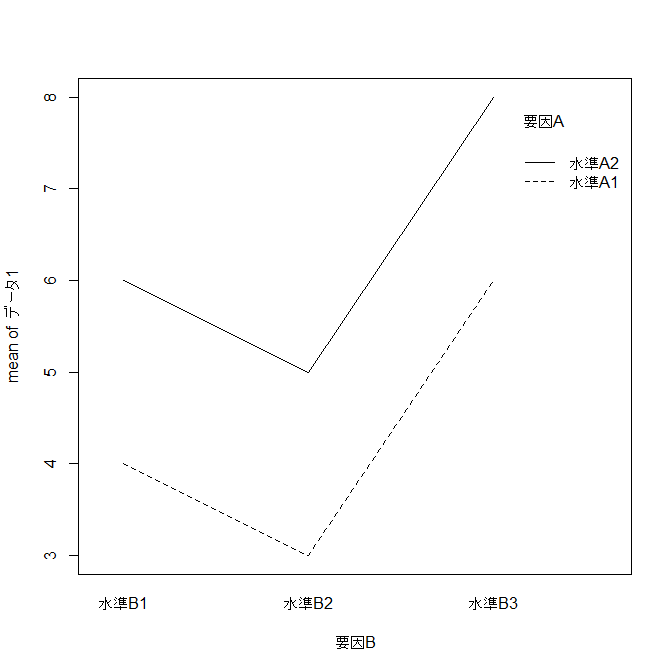
| パターンの例:
| | B1 | B2 | B3 |
| A1 | 4 | 3 | 6 |
| A2 | 4 | 6 | 7 |
|
要因Aによる平均値のプロット
|
要因Aによる平均値のプロット
|
要因Bによる平均値のプロット
|
要因Bによる平均値のプロット

|
手順の確認:
- 帰無仮説と対立仮説の設定
- 検定統計量の選択: 分散分析では、検定統計値としてFを利用
- 有意水準αの決定: 有意水準は5%、つまりα=0.05とする。この検定は片側検定
- 検定統計量の実現値を求める--- aov関数を用いて実現値を求める
- 帰無仮説の棄却or採択の決定
例題の「ミネラルウォーターの美味しさの評定に関する実験データ」に対して二元配置分散分析を行う :
を用いた計算方法の紹介
- 帰無仮説と対立仮説の設定
- 要因A(温度の違い)の主効果
- 帰無仮説H0:温度が違ってもおいしさ得点の母平均は等しい(要因Aの主効果はない)
- 対立仮説H1:温度の違いによっておいしさ得点の母平均は異なる(要因Aの主効果がある)
- 要因B(銘柄の違い)の主効果
- 帰無仮説H0:銘柄が違ってもおいしさ得点の母平均は等しい(要因Bの主効果はない)
- 対立仮説H1:銘柄の違いによっておいしさ得点の母平均は異なる(要因Bの主効果がある)
- 要因Aと要因Bの交互作用効果
- 帰無仮説H0:温度と銘柄の組み合わせによるおいしさ得点の影響はない(要因Aと要因Bの交互作用効果はない)
- 対立仮説H1:度と銘柄の組み合わせによるおいしさ得点の影響がある(要因Aと要因Bの交互作用効果がある)
- 検定統計量の選択 ---Fを検定統計量とする
- 有意水準αの決定: ここでは有意水準は5%、つまりα=0.05とする。片側検定である
- 検定統計量の実現値を求める: ここでは、最も一般的なaov関数を用いる
> 味 <- c(6,4,5,3,2,10,8,10,8,9,11,12,12,10,10,5,4,2,2,2,7,6,5,4,3,12,8,5,6,4)
> 温度 <- factor(c(rep("冷蔵庫",15),rep("常温",15)))
> 銘柄 <- factor(rep(c(rep("イカアン",5),rep("ボスビック",5),rep("ビビッテル",5)),2))
> summary(aov(味~温度*銘柄))
Df Sum Sq Mean Sq F value Pr(>F)
温度 1 67.5 67.500 21.3158 0.00011 ***
銘柄 2 155.0 77.500 24.4737 1.608e-06 ***
温度:銘柄 2 15.0 7.500 2.3684 0.11515
Residuals 24 76.0 3.167
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
- 帰無仮説の棄却or採択の決定:
- 温度の主効果:5%水準で有意な効果がある (p=0.0011 = 1.1×10-4)
- 銘柄の主効果:5%水準で有意な効果がある (p=1.6×10-6)
- 温度と銘柄の交互作用効果:5%水準で有意な効果はない(p=0.115)
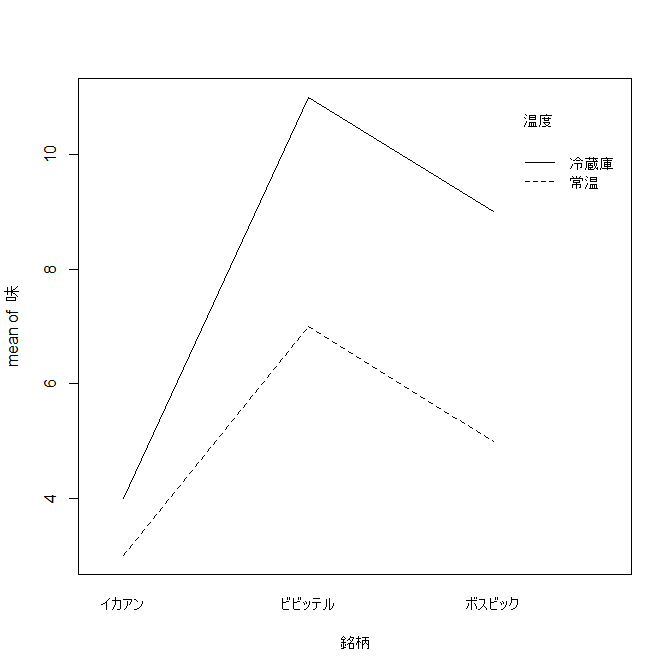
「interction.plot(横軸にとる要因、もう一方の要因、平均値を求める変数)」関数による交互作用効果の図:
interaction.plot(温度,銘柄,味)
[銘柄ごとの温度と味との関係の図]
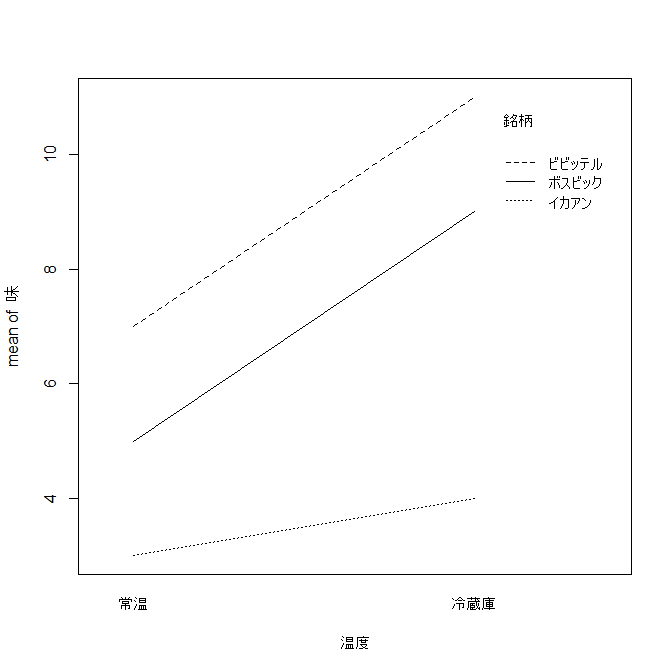
直線が完全に平行ではないので多少の交互作用はある(が有意な差ではない)
interaction.plot(銘柄,温度,味)
[温度ごとの銘柄と味との関係の図]
例題:ミネラルウォーターの美味しさの5人の評定者による評定データ(前の例題の表に評定者データを加えたもの):
| |
冷蔵庫 |
常温 |
| 評定者 |
イカアン |
ボスビック |
ビビッテル |
イカアン |
ボスビック |
ビビッテル |
| 村松 |
6 |
10 |
11 |
5 |
7 |
12 |
| 川崎 |
4 |
8 |
12 |
4 |
6 |
8 |
| 井口 |
5 |
10 |
12 |
2 |
5 |
5 |
| 松中 |
3 |
8 |
10 |
2 |
4 |
6 |
| 城島 |
2 |
9 |
10 |
2 |
3 |
4 |
同じ評定者が、温度と銘柄のそれぞれの要因の組合わせに対して評定を下す
> 人1 <- factor(rep(c("村松","川崎","井口","松中","城島"),6))
> 数字ID1 <- factor(rep(1:5,6))
> summary(aov(味~温度*銘柄
+Error(人1+人1:温度+人1:銘柄+人1:温度:銘柄)))
Error: 人1
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 4 45 11.25
Error: 人1:温度
Df Sum Sq Mean Sq F value Pr(>F)
温度 1 67.5 67.50 18 0.0132 *
Residuals 4 15.0 3.75
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: 人1:銘柄
Df Sum Sq Mean Sq F value Pr(>F)
銘柄 2 155 77.5 155 4.01e-07 ***
Residuals 8 4 0.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: 人1:温度:銘柄
Df Sum Sq Mean Sq F value Pr(>F)
温度:銘柄 2 15 7.5 5 0.039 *
Residuals 8 12 1.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
この例題の場合、「対応がある」ということは『個人差』によるデータのばらつきを分析することができる、ということ。
したがって(個人差のばらつきを除くことにより)、温度の主効果、銘柄の主効果、温度と銘柄の交互作用の効果の分析が得られる。
上の結果は、いずれも有意であることが示されています---対応なしの場合の分析結果と比較してみましょう。
例題:ミネラルウォーターの美味しさについての評定データ(一つ前の例題の表に評定者データを加えたもの):
| |
冷蔵庫 |
|
常温 |
| 評定者 |
イカアン |
ボスビック |
ビビッテル |
評定者 |
イカアン |
ボスビック |
ビビッテル |
| 村松 |
6 |
10 |
11 |
斉藤 |
5 |
7 |
12 |
| 川崎 |
4 |
8 |
12 |
和田 |
4 |
6 |
8 |
| 井口 |
5 |
10 |
12 |
寺原 |
2 |
5 |
5 |
| 松中 |
3 |
8 |
10 |
杉内 |
2 |
4 |
6 |
| 城島 |
2 |
9 |
10 |
新垣 |
2 |
3 |
4 |
同じ温度に対しては同じ評定者が銘柄のそれぞれの要因の組合わせに対して評定を下すが、冷蔵庫と常温では異なる評定者が評定する
> A1条件 <- rep(c("村松","川崎","井口","松中","城島"),3)
> A2条件 <- rep(c("斉藤","和田","寺原","杉内","新垣"),3)
> 人2 <- factor(c(A1条件,A2条件))
> 数字ID2 <- factor(c(rep(1:5,3),rep(6:10,3)))
> summary(aov(味~温度*銘柄
+Error(人2:温度+人2:温度:銘柄)))
Error: 人2:温度
Df Sum Sq Mean Sq F value Pr(>F)
温度 1 67.5 67.5 9 0.0171 *
Residuals 8 60.0 7.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: 人2:温度:銘柄
Df Sum Sq Mean Sq F value Pr(>F)
銘柄 2 155 77.5 77.5 5.87e-09 ***
温度:銘柄 2 15 7.5 7.5 0.00504 **
Residuals 16 16 1.0
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
警告メッセージ:
In aov(味 ~ 温度 * 銘柄 + Error(人2:温度 + 人2:温度:銘柄)) :
Error() model is singular
対応のない分散分析で「残差」としてまとめられていたものを次の要因に分解
各評定者は同じ温度の条件で3種類の銘柄を飲んでいる⇒個人差の要因
だから、個人差の要因である「人2」と温度の違いの要因をあらわす「温度」が関係する組み合わせだけを指定する
この分析の結果、「温度」の主効果と「銘柄」の主効果、「温度」と「銘柄」の交互作用効果に有意差が認められている
| 目的 |
関数名と書式 |
使い方 |
| 二元配置分散分析(対応なし)を行う |
summary(aov(y ~ a*b)) |
summary(aov(y ~ a*b))⇒ aとbは要因、yは従属変数
|
| 交互作用効果を確認するための平均値のプロットを作成する |
interaction.plot(a,b,y) |
interaction.plot(a,b,y)⇒ aは横軸に取る要因、bは線で表す要因、yは縦軸に取る従属変数(平均値を求める変数)
|
| 二元配置分散分析(2要因とも対応あり)を行う(2) |
summary(aov(y ~ a*b+Error(t+t:a+t:b+t:a:b)) |
summary(aov(y ~ a*b+Error(t+t:a+t:b+t:a:b)⇒ aとbは要因、yは従属変数, tは繰り返しの要因
|
| 二元配置分散分析(1要因のみ対応あり)を行う(2) |
summary(aov(y ~ a*b+Error(t:a+t:a:b)) |
summary(aov(y ~ a+b))⇒ aとbは要因、yは従属変数, tは繰り返しの要因
|
問題(1) (教科書」p.201の演習問題2)
Ex7-1.csvはCSV形式のファイルであり、教科書p.201の表7.12のデータが収められている。
このデータを読み込み、講義、問題、実習、それぞれの授業形態によって成績に差があるかどうか、有意水準5%で分散分析せよ。
注: これは一元配置分散分析の問題
[
数値を集めて変数にセットする]
この問題は一元配置分散分析の問題なので、
Rで統計学を学ぶ(6)で学んだように、
- 成績すべてを配列にして変数(例えばSeiseki)にセットする
- その要素の並びに対応する人リストを作る。ここで、
factor関数を適用するのを忘れないように。factor関数を適用して
えられたリストを変数(例えば Person)にセットする。
- その要素の並びに対応する授業形態リストを作る。ここでも
factor関数を適用するのを忘れないように。
factor関数を適用してえられたリストを変数(例えば Lecture)にセットする。
- summary(aov(Seiseki ~ ...))というようなRの関数を実行する
とやればよい。ここで、「成績すべてを配列にして変数にセット」
の方法で困っている人が多い。
その方法とは、各行の成績をまず取り出して、
それを結合しようとしていたのである。
この「各行の要素を取り出した配列を作る」
のを一つの関数で実現するやり方は私も知らない(
もちろん、一つの関数ではなくfor文を使えばできる)。
しかし、
列の要素を取り出すのは簡単にできるのである。
目的、すべての成績を一つの配列にまとめる、ことにあるのだから、
行ではなく列の方向で取り出すことを考えよう。
ちなみにその方法とは(csvファイルを読み込んで変数 data にセットしたとする)
「
data$森本」
と書く方法である。これで、森本氏の成績が配列となって取り出せる。
だから、すべての成績は、
Seiseki <- c( data$森本, data$田中, data$稲葉,data$瀬木,data$高橋,data$工藤,data$金子)
なおこれは次のようにしてもできる:
a <- c( data[,2], data[,3], data[,4], data[,5], data[,6], data[,7], data[,8])
もしくは
Seiseki <- c()
for (i in 2:ncol(data))
Seiseki <- c(Seiseki, data[,i])
として取り出せる
なお同じように、次のようにすれば行ごとに要素を取り出してこられる:
size <- ncol(data)
a <- as.integer(c( data[1,2:size], data[2,2:size], data[3,2:size] ))
もしくは
Seiseki <- c()
for (i in 1:nrow(data))
Seiseki <- c(Seiseki, as.integer(data[i,2:ncol(data)]))
ここでは
as.integer関数により「数」にするのがミソである。
問題(2)
Ex7-2.csvはCSV形式のファイルであり、3つの学部(工学部、経済学部、教育学部)と曜日(月~金)
による出席率(%)のデータである。
このデータを読み込み、学部と曜日による出席率に差があるかどうか、有意水準5%で分散分析せよ。
(出典: 長畑(2009)『Rで学ぶ統計学』共立出版)
注: これも一元配置分散分析の問題
問題(3)
goggles.csvはCSV形式のファイルであり、
アルコール(alcohol)の摂取(0, 2、4杯)と男女の性別(gender)により、魅力度(attractiveness)がどのように変わるかを調べたデータである。
このデータを読み込み、性別とアルコールの摂取によって魅力度に差があるかどうか、有意水準5%で分散分析せよ(主効果および交互作用効果を調べよ)。
(出典: Field, A. , Miles, J. & Field, Z. (2012)
Discovering Statistics Using R. Sage.
問題(4)
早稲田大学向後先生による分散分析の問題を解きなさい。
問題(5)
1要因のみ対応のある二元配置分散分析を必要とするテーマ(状況設定)を考えよ。
これは、自分や研究室の研究テーマ、実験のテーマなどから採取するのが望ましい。
どのようなことを主張、もしくは判断・調査するために、
どのようなデータを採取したか、またその要因(2つあるはず)
とそれぞれの水準(2つ以上あるはず)について説明せよ。
また、それが「2要因とも対応がある」とは言えないのかも説明せよ。
なお、二元配置分散分析の問題設定が難しい場合は、
一元配置分散分析でもよいものとする(が、評価は低くなる)。