Rで統計学を学ぶ(6)
この講義では、教科書の第7章「分散分析」のうち、7.1と7.2「一元配置分散分析」をとりあげます。
6章のt検定は2つの群の平均値を比較しましたが、分散分析は3つ以上の群の平均値を比較したり、ある条件の違いによって母平均が異なるかを検定します。
このウェブページと合わせて教科書を読み進めてください。
学習項目です:
分散分析(ANOVA, Analysis Of Variance)
とは、3つ以上の群の平均値差の検定や、条件(の組み合わせ)の違いによって母平均が異なるかどうかを検定する方法です
(注意:「分散」という名前に惑わされないように)
注: ここでは7.1.2節の説明を先に行います.
データにおいて変数がとる値は、以下の『要因』によるものと「誤差」によるものがあるとみなせます:
- 要因: 母平均に違いをもたらす原因
- 水準: ある要因の中に含まれる個々の条件
そして、
「データ全体のばらつき」は、『要因によるばらつき』と『誤差によるばらつき』の和とみなせます。分散分析は、データ全体のばらつきを「平方和」として表し、それを要因ごとに分け、誤差に比べて大きな影響を与えている要因を探し出し、推測に利用する方法です。
具体的には、ある要因の水準ごとに分けたデータ(群)について、それぞれの群の平均を求めます。そして全データに対し、その群の平均を引いた差の2乗を求めます。Rで書くと(「全データ」変数に行列としてデータが入っているとします):
A <- c(15,9,18,14,18)
B <- c(13,8,8,12,7)
C <- c(10,6,11,7,12)
D <- c(10,7,3,5,7)
全データ <- cbind(A,B,C,D)
群平均 <- colMeans(全データ)
群平均行列 <- matrix(rep(群平均, nrow(全データ)), nrow=nrow(全データ),
ncol=ncol(全データ),byrow=TRUE)
群内 <- 全データ - 群平均行列
群内平方和 <- sum(群内^2)
分母 <- 群内平方和 / ( (nrow(全データ)-1)*ncol(全データ) )
このように「それぞれのデータと群平均との差の2乗の和」が「群の中のデータのばらつき」を表し、これが(
群内平方和)と呼ばれるものです。そして、これを群内の自由度(「各群のデータ数-1」の和)で割ったものが、各データの「
誤差によるばらつき」を表しているとみなすことができます。
一方、「要因によるばらつき」は、群間のばらつきで表されます。それは「全データの平均と各群の平均の差」の2乗の和を、群間の自由度(群の数-1、つまり水準数-1)で割った値と計算されます:
全体平均 <- sum(colMeans(全データ))/ncol(全データ)
群間 <- matrix(rep(群平均 - 全体平均, nrow(全データ)),nrow(全データ), byrow=TRUE)
群間平方和 <- sum(群間^2)
分子 <- 群間平方和 / (ncol(全データ) - 1)
群間平方和を群間の自由度で割った値(「分子」の値)が『
要因によるばらつき』です。これを「誤差によるばらつき」で割った値が
Fであり、Fの値によって要因のばらつきの影響を推定するのが分散分析です(この計算方法が「分散」という名前がついている理由です)。
> 分子
[1] 61.33333
> 分母
[1] 8.625
> ( F <- 分子/分母 )
[1] 7.111111
変数の値に影響を及ぼす要因が1個の場合
一元配置法、要因が2個の場合
二元配置法、
3個以上の場合は
多元配置法という。
また要因と水準の組み合わせごとに実験が繰り返されてデータがとられる場合を
繰り返しのある二元配置法などと呼ぶ。
検定の結果として表示される分散分析表の構成:
| 要因 |
自由度(Df) |
平方和(Sum Sq) |
平均平方(Mean Sum Sq) |
F値(F value) |
P値 |
評価 |
| 要因名 |
水準数-1 |
群間平方和 |
群間平方平均 |
F値 |
p値 |
印(表の下に説明) |
| 残差(Residuals) |
水準数×(1群あたりのデータ数-1) |
群内平方和 |
群内平方平均 |
|
|
|
| 合計 |
データ数-1 |
|
|
|
|
|
評価の印: 星印は有意(***は0.1%、**は1%、*は5%水準)、.は10%(「有意傾向」という)を表す
例題:以下の表は『教え方』ごとにみた統計学テストの成績である。この表から、4通りの教え方(A,B,C,D)によって統計学テストの母平均に差があるだろうか?
| A |
B |
C |
D |
| 15 |
13 |
10 |
10 |
| 9 |
8 |
6 |
7 |
| 18 |
8 |
11 |
3 |
| 14 |
12 |
7 |
5 |
| 18 |
7 |
12 |
7 |
この標本が母平均の等しい4群から抽出される可能性が高いかどうかを検討するために分散分析を行う。ここで『教え方』が
要因、A, B, C, Dの4つがその
水準となる.
Rを用いた計算方法の紹介
- 帰無仮説と対立仮説の設定
・帰無仮説 H0:4群の母平均は等しい
・対立仮説 H1:4群の母平均は等しくない
注意: 4群のうち1つだけ母平均が異なるような場合でも対立仮説は成立
- 検定統計量の選択 ---
次のFを検定統計量とする:

これは帰無仮説(すべての群の母平均が等しいとき)のもとで、F分布に従う
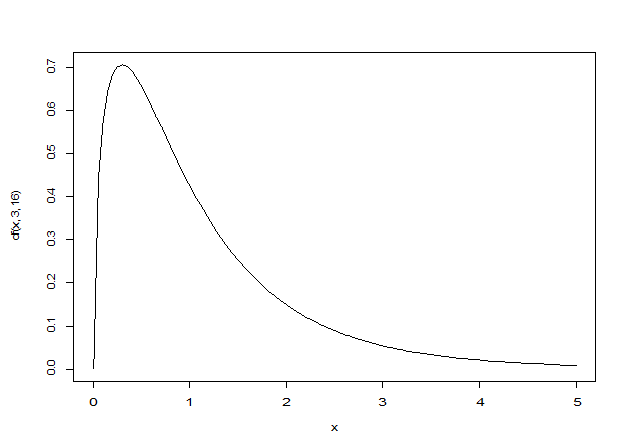 F分布の自由度は2種類:分子と分母の自由度
F分布の自由度は2種類:分子と分母の自由度
F分布の描画: df(x,分子の自由度,分母の自由度) 関数を使用
curve(df(x, 3, 16), 0, 5)
- 有意水準αの決定: ここでは有意水準は5%、つまりα=0.05とする
F分布のグラフから明らかなように、F分布は正値を取る⇒ 分散分析は常に片側検定
- 検定統計量の実現値を求める: 以下の3種類を紹介
- oneway.test関数 : 一元配置分散分析のみ実行可能
- aov関数: 最も一般的
- anova関数: 複数のモデルの比較など高度な分析に対応
Rを用いた計算:
> A <- c(15,9,18,14,18)
> B <- c(13,8,8,12,7)
> C <- c(10,6,11,7,12)
> D <- c(10,7,3,5,7)
> 統計テスト2 <- c(A,B,C,D)
> 指導法 <- c(rep("A",5),rep("B",5),rep("C",5),rep("D",5))
> 指導法2 <- factor(指導法)
> 指導法2
[1] A A A A A B B B B B C C C C C D D D D D
Levels: A B C D
以上で準備ができたので、「帰無仮説の棄却/採択の決定」も含めて検定統計量の実現値を求める:
oneway関数
> oneway.test(統計テスト2 ~ 指導法2, var.equal=TRUE )
One-way analysis of means
data: 統計テスト2 and 指導法2
F = 7.1111, num df = 3, denom df = 16, p-value = 0.002988
母分散が等質と仮定したoneway.test関数の結果、F値は7.11、p値が0.003であるから、帰無仮説が棄却される
aov関数
> aov(統計テスト2 ~ 指導法2)
Call: aov(formula = 統計テスト2 ~ 指導法2)
Terms:
指導法2 Residuals
Sum of Squares 184 138
Deg. of Freedom 3 16
Residual standard error: 2.936835
Estimated effects may be unbalanced
> summary(aov(統計テスト2~指導法2))
Df Sum Sq Mean Sq F value Pr(>F)
指導法2 3 184.000 61.333 7.1111 0.002988 **
Residuals 16 138.000 8.625
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
aov関数により分散分析表が表示される。この表では、F値が7.11、p値が 0.003 であるから、帰無仮説が棄却される。
anova関数
> anova(lm(統計テスト2 ~ 指導法2))
Analysis of Variance Table
Response: 統計テスト2
Df Sum Sq Mean Sq F value Pr(>F)
指導法2 3 184 61.333 7.1111 0.002988 **
Residuals 16 138 8.625
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
aov関数と同様に、分散分析表が出力される。F値は7.11、p値は 0.003 であるから、帰無仮説が棄却される。
実際に使うのは、上の3つの方法のどれを使ってもよい。すべて帰無仮説が棄却されたことから、検定の結果、4つの指導方法の間に有意な平均値差が見られたことが導ける。
多重比較(Tukeyの方法)
一元配置分散分析の結果「帰無仮説が棄却」されても、これだけでは「群の母平均が等しくない」ことしかわからない。
具体的に「どの群とどの群の間に差があるか」を知りたいことが多い。それには
多重比較を行う。ここでは
Tukey(テューキー)の方法を紹介
仮定: 各群のデータ数(サンプルサイズ)nが等しく、各群の母分散も等しい(分散の等質性)
検定統計量q: 
Rを用いて説明:指導法AとDの比較
> mean(A)
[1] 14.8
> mean(D)
[1] 6.4
> nrow(全データ)
[1] 5
> 群内平均平方
[1] 8.625
> q <- abs(mean(A)-mean(D))/sqrt(群内平均平方/nrow(全データ))
> q
[1] 6.395651
> qtukey(0.95,4,16)
[1] 4.046093
> qtukey(0.05,4,16,lower.tail=FALSE)
[1] 4.046093
この結果、qの実現値は棄却域の中にあるので(q > 4.05)、指導法Aと指導法Dの間に5%水準で有意差あり
次のようにTukeyHSD (Tukey's
Honest Significant Difference
)関数を用いれば、いろいろな指導方法による平均値差の多重比較が可能
> TukeyHSD(aov(統計テスト2 ~ 指導法2))
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = 統計テスト2 ~ 指導法2)
$指導法2
diff lwr upr p adj
B-A -5.2 -10.514108 0.1141085 0.0562227
C-A -5.6 -10.914108 -0.2858915 0.0371222
D-A -8.4 -13.714108 -3.0858915 0.0017736
C-B -0.4 -5.714108 4.9141085 0.9963241
D-B -3.2 -8.514108 2.1141085 0.3446966
D-C -2.8 -8.114108 2.5141085 0.4561325
出力された表においてp値が0.05以下のものに注目する: C-AとD-Aの間に5%水準で有意差がある。
(B-Aも5%に近い差があることから、Aだけが他のB,C,Dと差があったことが分かる)
コンピュータ演習室のコンピュータでこれを走らせたところ、
「不正なマルチバイト文字があります」というエラーになりました。
こういう場合は「日本語で表記された変数」を使わず、以下のようにしてください。
> test <- 統計テスト2
> method <- 指導法2
> TukeyHSD(aov(test ~ method))
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = test ~ method)
$method
diff lwr upr p adj
B-A -5.2 -10.514108 0.1141085 0.0562227
C-A -5.6 -10.914108 -0.2858915 0.0371222
D-A -8.4 -13.714108 -3.0858915 0.0017736
C-B -0.4 -5.714108 4.9141085 0.9963241
D-B -3.2 -8.514108 2.1141085 0.3446966
D-C -2.8 -8.114108 2.5141085 0.4561325
表記以外は同じ結果が得られます
一元配置分散分析(対応あり)では、同じ被験者が複数の条件を経験する(
被験者内計画のデータ)というような対応があるデータを対象とする
[
対応のあるなしの違い]
データに『対応がある』ということは、それだけ情報が多い(データのばらつきが揃っている「はず」)のだから、それを用いた検定が可能になります。前章で「対応のあるt検定」について述べ、そこで取り上げた例題では結論は変わらなかったものの、対応のある検定の方がp値が小さい、ということを見ました。
ここで取り上げる例題でも同じようなことがわかります。以下ではデータに「対応がない」ものとして検定した結果を載せます。
> 好意度 <- c(7,8,9,5,6,5,4,7,1,3,8,6,7,2,5)
> 科目 <- factor(c(rep("線形代数",5),rep("微分積分",5),rep("確率統計",5)))
> summary(aov(好意度~科目))
Df Sum Sq Mean Sq F value Pr(>F)
科目 2 22.53 11.267 2.641 0.112
Residuals 12 51.20 4.267
『対応のない』データとしての検定は、F値が2.64で、p値は0.112なので、有意水準0.05よりも大きいため、
帰無仮説は棄却されない。
この結果と、本文で述べる「対応がある」場合の結果とを比べてみてください。
例題: 以下の表は5名の学生に、線形代数、微分積分、確率統計に対する好意度の評定データである。
これら3つの科目に対する好意度に差があるだろうか?(念のため:これは1要因3水準)
| 学生 |
線形代数 |
微分積分 |
確率統計 |
| 田中 |
7 |
5 |
8 |
| 岸 |
8 |
4 |
6 |
| 大引 |
9 |
7 |
7 |
| 吉川 |
5 |
1 |
2 |
| 荻野 |
6 |
3 |
5 |
Rを用いた計算方法の紹介
- 帰無仮説と対立仮説の設定
- 帰無仮説 H0:3科目の好意度の母平均は等しい
- 対立仮説 H1:3科目の好意度の母平均は等しくない
- 検定統計量の選択 ---
次のFを検定統計量とする:

これは帰無仮説(すべての群の母平均が等しいとき)のもとで、F分布に従う
- 有意水準αの決定: ここでは有意水準は5%、つまりα=0.05とする
F分布のグラフから明らかなように、F分布は正値を取る⇒ 分散分析は常に片側検定
- 検定統計量の実現値を求める: ここでは、最も一般的なaov関数を用いる:
> 好意度 <- c(7,8,9,5,6,5,4,7,1,3,8,6,7,2,5)
> 科目 <- factor(c(rep("線形代数",5),rep("微分積分",5),rep("確率統計",5)))
> 人 <- factor(rep(c("田中","岸","大引","吉川","萩野"),3))
> summary(aov(好意度~科目+人))
Df Sum Sq Mean Sq F value Pr(>F)
科目 2 22.533 11.267 14.696 0.002095 **
人 4 45.067 11.267 14.696 0.000931 ***
Residuals 8 6.133 0.767
---
Signif. Codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
[『人』がなぜ必要?もしくは「好意度~科目+人」の意味]
まず『人』を含めないaovの結果を示しましょう---これはデータに「対応がない」ときの分析と同じものです:
> summary(aov(好意度~科目))
Df Sum Sq Mean Sq F value Pr(>F)
科目 2 22.53 11.267 2.641 0.112
Residuals 12 51.20 4.267
これが示すように、科目の効果だけでは好意度の平均に有意な差が認められません。
そもそもこのデータにおいて『対応がある』というのは、好意度のデータが個人別だったからです。
言い換えれば、「好意度」データを説明する要因として『科目』と『人』があり、『人』を考慮することでデータに「対応がある」と認められたのです。それをRでは
好意度 ~ 科目+人と表したのです。
- 帰無仮説の棄却か採択かの決定: 結果の出力の「科目」の行において、p値が 0.0021 と得られているので、5%の有意水準で、
科目間に有意な差があることが認められた。
参考:3群以上を比較するとき、2群間の検定(T検定)を使ってはいけない理由
分散分析なら1遍に済むのに、T検定の場合3通りやらなければならないから、
というのが理由ではもちろんありません。
いま、A,B, Cという3つの群があったとします。そこで、2群間の検定を
A-B間、B-C間、C-AC間で有意水準5%で行ったとします。
ここで、「この組み合わせの少なくとも1つは有意差がある」
となる確率を計算すると(実際にその間に有意差があるなしに拘らず)、
1-(1-0.05)*(1-0.05)*(1-0.05) = 0.14
となります。つまり、
有意水準 5% (=0.05)で検定したつもりが、
この方法では実質的に 14 %で検定している、つまり
検定力が低下してしまう、というのが理由です。
| 目的 |
関数名と書式 |
使い方 |
| 要因型ベクトルに変換 |
factor(x)
| factor(指導法)
⇒ 文字型ベクトルである「指導法」を要因型ベクトルに変換する
|
| 行列を作る |
matrix(ベクトル, nrow, ncol)
| matrix(c(1,2,3,4,5,6),nrow=2, ncol=3)
⇒ c(1,2,3,4,5,6)というベクトルから2行3列の行列を作る
|
| 行列の列数を数える |
ncol(行列)
| ncol(行列データ)
⇒ 「行列データ」の列の数を返す
|
| 行列の行数を数える |
nrow(行列) |
nrow(行列データ)
⇒ 「行列データ」の行の数を返す
|
| データ(列ベクトル)を横に追加し行列を作る |
cbind(ベクトル1, ..., ベクトルn)
| cbind(A,B,C,D)
⇒ A~Dは列ベクトル、これらをつなげて行列を作る。行ベクトルをつなげて行列を作る場合は rbind関数を使う
|
| 行列の列ごとに平均を求める |
colMeans(行列
| colMeans(全データ)⇒ 行列「全データ」の各列ごとの平均を計算し、ベクトルを返す。
各業ごとの平均を計算してベクトルを返す関数は rowMeans
|
| 繰り返しのデータを作る |
rep(データ, 回数) |
rep("A",8⇒ 「A」を8回繰り返したデータを作る |
| 一元配置分散分析(対応なし)を行う(1) |
oneway.test(y ~ x) |
oneway.test(y~x, var.equal=TRUE)
⇒ xは要因、yは従属変数、var.equal=TRUEで分散の等質性を仮定
|
| 一元配置分散分析(対応なし)を行う(2) |
summary(aov(y ~ x)) |
summary(aov(y ~ x))⇒ xは要因、yは従属変数
|
| 一元配置分散分析(対応なし)を行う(3) |
anova(lm(y ~ x)) |
anova(lm(y ~ x))⇒ xは要因、yは従属変数 |
| F分布の確率密度関数 |
df(x, df1, df2) |
df(x, df1, df2)⇒ 分子の自由度df1, 分母の自由度df2のF分布の確率密度関数を返す |
| F分布で下側確率に対応する値を求める |
qf(p, df1, df2) |
qf(0.095, 3, 16)⇒ 分子の自由度3, 分母の自由度16のF分布で下側確率0.95となるFの値を求める。
上側確率に対応するF値を求めるには、lower.tail=FALSEとオプション指定する |
| テューキーの多重比較のためqの臨界値を求める |
qtukey(p, k, df) |
qtukey(0.95, 4, 16)⇒ 比較する群の数4, 群内の自由度16のとき、下側確率0.95に対するqの値を求める。
上側確率に対応するqの値を求めるにはlower.tail=FALSEとオプション指定する |
| テューキーの多重比較を行う |
TukeyHSD(aov(y ~ x)) |
TukeyHSD(aov(y ~ x))⇒ 分散分析の結果aov(y~x)を引数に指定して、多重比較を行う |
| 一元配置分散分析(対応あり)を行う |
summary(aov(y ~ x+t)) |
summary(aov(y ~ x+t))⇒ xは要因、yは従属変数、tは繰り返しの要因 |
教科書 p.201 問題(1)
ある大学の4学部から8名ずつの学生を無作為抽出して得られた結果が以下である。学部間でテストの母平均に差があるかどうか、
有意水準5%で分散分析を行え。
法学部 <- c(75, 61, 68, 58, 66, 55, 65, 63)
文学部 <- c(62, 60, 66, 63, 55, 53, 59, 63)
理学部 <- c(65, 60, 78, 52, 59, 66, 73, 64)
工学部 <- c(52, 59, 44, 67, 47, 53, 58, 49)
問題(2)
shidouhou.csvはCSV形式のファイルであり、教科書p.38-39のデータが収められている。
このデータを読み込み、統計テスト1の成績が男女の違いで差があるかどうか、また統計の好き嫌いで差があるかどうかをそれぞれ検定せよ。
[
参考: csvファイルを読み込む (再掲)]
区切り記号がコンマのcsvファイルを読み込み、その内容をデータフレームとして取り込むには、
read.csv関数を用いる。
もっとも中にはちゃんと読み込めないこともあるので、値を確認すること。
そして読み込めない場合は、区切り記号を適切なものにセットしたり、
他の read.table というような関数を使ってみることも考えよう。
問題(3)
下は小学校1年生から6年生まで、各学年から5人ずつ無作為抽出し、50メートル走のタイムを計測したデータである。学年による違いがあるか、検討せよ(出典: 長畑(2009)『Rで学ぶ統計学』共立出版)
一年生 <- c(11.3, 12.4, 15.5, 13.6, 12.4)
二年生 <- c(12.3, 13.4, 11.5, 11.6, 10.8)
三年生 <- c(9.2, 10.4, 8.6, 9.8, 10.7)
四年生 <- c(9.5, 8.4, 9.8, 10.4, 7.8)
五年生 <- c(8.4, 7.5, 8.6, 7.9, 8.3)
六年生 <- c(7.8, 8.5, 7.6, 7.2, 7.5)
問題(4)
下は3種類の1500ccの乗用車を繰り返し4回走行させ、その1リットルあたりの走行距離(燃費)を計測したものである。
車種による違いがあるか、分散分析せよ。(出典: 長畑(2009)『Rで学ぶ統計学』共立出版)
A <- c( 8.0, 9.0, 7.0, 6.0)
B <- c(12.0, 11.0, 13.0, 12.0)
C <- c( 9.0, 10.0, 9.0, 8.0)
Rで統計学(5) トップページに戻る Rで統計学(7)


