SVMの理解¶
目的¶
- この章では
- サポートベクターマシン(SVM)の概念を理解する.
理論¶
線型分離可能なデータ¶
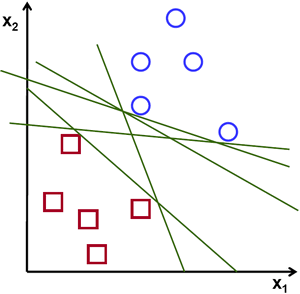
青と赤の2種類のデータが現れる下図のような状況について考えてみよう.k近傍法ではテストデータに対し、学習データそれぞれとの距離を測り,その距離が最小となる学習データをクラス分類の結果としていた.このような方法では、距離を求めるのに長い時間がかかり,すべてのデータを記憶するのに多くの記憶容量が必要である。しかし、図で与えられているデータについて考えてみると,そこまでする必要があるのだろうか?
別な方法を考えてみよう.学習データを2つの領域に分割するような直線, 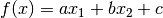 を見つけよう.そして新しいテストデータ
を見つけよう.そして新しいテストデータ 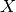 に対しては,先ほど得た直線の式
に対しては,先ほど得た直線の式 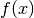 を使う。もしも
を使う。もしも 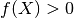 であれば
であれば 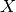 は青クラスに属し、そうでなければ赤クラスに属す.この直線を 決定境界(Decision Boundary) と呼ぶ.この方法はとても単純で記憶容量的にも効率がよい.そして、1つの直線(高次元であれば超平面)によって2つのグループに分割できるデータのことを 線型分離可能(Linear Separable) という.
は青クラスに属し、そうでなければ赤クラスに属す.この直線を 決定境界(Decision Boundary) と呼ぶ.この方法はとても単純で記憶容量的にも効率がよい.そして、1つの直線(高次元であれば超平面)によって2つのグループに分割できるデータのことを 線型分離可能(Linear Separable) という.
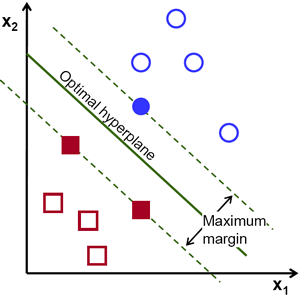
上の図の状況だと、実はそのような直線はたくさん存在する。そうなると、どのような直線を選べばよいだろうか? 直感的には,どの点からもできるだけ離れたところを通るような直線を選ぶべきだと言える。その理由は、データにはノイズが含まれる可能性があるからである.これが分類の精度に影響しないようにすべきである。どの点からも遠いところを通る直線を選べば、ノイズを含むデータに対して頑健性がありそうである。そこで,サポートベクターマシン(SVM)が行っているのは、直線(超平面)と学習データの距離において「最小の距離を最大化する」直線(超平面)を見つけることである.次の図において、中心を通る太い直線がその候補である:
決定境界を見つけるには、学習データが必要である.ただし全部のデータは必要ではない.学習データのうち、クラスが異なるデータとの距離が近いデータさえあればよい.例として示した上の図では,青く塗りつぶされた円と赤く塗りつぶされた四角があればよいのである.これらを サポートベクター(Support Vectors) と呼び,サポートベクターの間を通る直線を サポートプレーン(Support Planes) と呼ぶ. サポートベクターは決定境界の計算に適している。全データを保持する必要はない。そのためデータ削減になる.
まず初めにデータを最も良く表現する二つの超平面を見つける.上の図で言うと,青のデータは 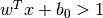 という超平面によって表され,赤のデータは
という超平面によって表され,赤のデータは 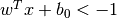 という超平面で表される.ここで,
という超平面で表される.ここで, 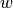 は 重みベクトル(weight vector) (
は 重みベクトル(weight vector) ( ![w=[w_1, w_2,..., w_n]](../../../../_images/math/3f85eb04600da2130fdd6b9a08a01437b9e9646a.png) ),
), 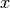 は特徴ベクトル (
は特徴ベクトル (![x = [x_1,x_2,..., x_n]](../../../../_images/math/2191d7168dbb9daf9d46b22e43b81bb2e5f9c401.png) ),
), 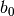 は バイアス(bias) を表す.重みベクトルは決定境界の傾きを表し,バイアスは決定境界の位置を表すパラメータである.
決定境界はこの2つの超平面の中間として定義される.すなわち,
は バイアス(bias) を表す.重みベクトルは決定境界の傾きを表し,バイアスは決定境界の位置を表すパラメータである.
決定境界はこの2つの超平面の中間として定義される.すなわち, 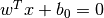 と表現できる.サポートベクターから決定境界までの最小距離は
と表現できる.サポートベクターから決定境界までの最小距離は
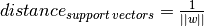
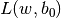 をある制約条件のもとで最小化しなければならず、これは次のように表される:
をある制約条件のもとで最小化しなければならず、これは次のように表される:

ここで ![t_i \in [-1,1]](../../../../_images/math/6513fc85b1daf439bb5a4ab1ea313ae91358bb41.png) は各クラスのラベルを意味する.
は各クラスのラベルを意味する.
注: 青クラスはti=1で、 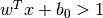 を満たすので、subject toの右にある制約を満たす。また赤クラスはti=-1で、
を満たすので、subject toの右にある制約を満たす。また赤クラスはti=-1で、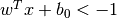 を満たすので、これも制約を満たす。つまり上記の制約は学習データがちゃんと超平面で分類されているという条件を表す、その上でマージン最大⇒(
を満たすので、これも制約を満たす。つまり上記の制約は学習データがちゃんと超平面で分類されているという条件を表す、その上でマージン最大⇒(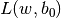 はその逆数なので)
はその逆数なので)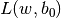 最小、という条件となる。)
最小、という条件となる。)
非線形分離可能データ¶
一つの直線では分離不可能なデータを考えてみよう.例えば,’X’ が-3と+3,’O’が -1と+1という値を取る1次元のデータを考える.この状況では明らかにXとOのクラスはは線型分離不可能である。しかし,このようなデータでさえも分類の方法がある.それは、このデータセットを例えば 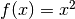 という関数で写像する、という方法である。このようにすれば’X’ は 9,’O’ は1となるため、線型分離可能となる.
という関数で写像する、という方法である。このようにすれば’X’ は 9,’O’ は1となるため、線型分離可能となる.
別な方法としては、データを1次元から2次元へと変換する方法がある.例えば関数 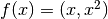 を使って写像すると, ‘X’ は(-3,9)と(3,9)となり,’O’は(-1,1)と(1,1)となる.この写像後のデータも線型分離可能である.要するに,低次元空間では線形分離不能なデータでも、高次元空間に写像すれば線型分離可能となる可能性があるのである.
を使って写像すると, ‘X’ は(-3,9)と(3,9)となり,’O’は(-1,1)と(1,1)となる.この写像後のデータも線型分離可能である.要するに,低次元空間では線形分離不能なデータでも、高次元空間に写像すれば線型分離可能となる可能性があるのである.
一般的に,あるd次元空間のデータを別のD次元空間 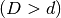 のデータに写像して、線型分離可能かどうか調べることは可能である.ここで、高次元(カーネル)空間における内積(dot product)計算を、低次元入力(特徴)空間における内積計算で簡単化するというアイデアがある.次の例でこれを説明する.
のデータに写像して、線型分離可能かどうか調べることは可能である.ここで、高次元(カーネル)空間における内積(dot product)計算を、低次元入力(特徴)空間における内積計算で簡単化するというアイデアがある.次の例でこれを説明する.
2次元空間中の2点 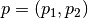 と
と 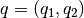 を考えよう.そして2次元の点を3次元空間に写像する関数
を考えよう.そして2次元の点を3次元空間に写像する関数 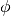 を次のように定義する:(注: 2つ書いてあるが定義は同じである)
を次のように定義する:(注: 2つ書いてあるが定義は同じである)
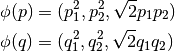
ここで2点の内積を計算する「カーネル」関数 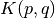 を次のように定義しよう:
を次のように定義しよう:
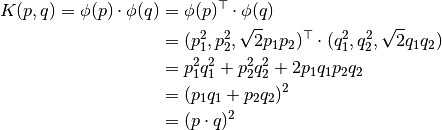
つまり、関数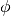 により2次元空間のデータを3次元空間に写像した2点の内積が、元の2次元空間のデータの内積の2乗によって計算できるのである.この計算方法は,より高次元空間でも適用可能である.つまり,高次元の特徴ベクトルの内積計算を低次元空間における計算で置き換えられるのである.特徴ベクトルの写像により、計算コストを抑えたまま,高次元空間が使えることになる.
により2次元空間のデータを3次元空間に写像した2点の内積が、元の2次元空間のデータの内積の2乗によって計算できるのである.この計算方法は,より高次元空間でも適用可能である.つまり,高次元の特徴ベクトルの内積計算を低次元空間における計算で置き換えられるのである.特徴ベクトルの写像により、計算コストを抑えたまま,高次元空間が使えることになる.
さて今度は誤分類の問題について考えよう.ただ単にマージンを最大化する決定境界を求めるだけでは十分ではない。誤分類による誤りの問題も考慮しなければいけない.時にはマージンが最大ではなくても誤分類を減らせるような決定境界が存在することがある.とにかく,私たちは最大マージンであると共に誤分類が少なくなるような決定領域を求めるモデルへと修正する必要がある.そのため最小化の基準を以下のように変更する:(注: カッコの中に書いてあるのは、「誤分類データと正解領域との距離(の和)」)
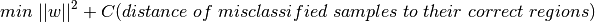
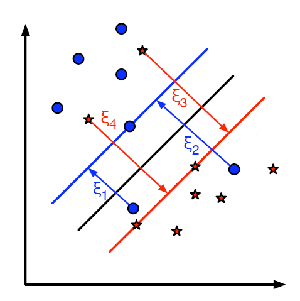
- 下図はこの考え方を示している.学習データのサンプル点それぞれに対し、新しいパラメータ
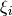 を定義する.このパラメータは対応する学習サンプルとその正しい決定領域との距離を表す.誤分類されていないサンプル点は、対応するサポートプレーンにあるため、距離はゼロであるので、これが問題になるのは誤分類データだけである.そこで、ξ1からξ4までの長さの和に定数Cをかけたものと||w||2との和を最小にするというのが最適化問題になる。
を定義する.このパラメータは対応する学習サンプルとその正しい決定領域との距離を表す.誤分類されていないサンプル点は、対応するサポートプレーンにあるため、距離はゼロであるので、これが問題になるのは誤分類データだけである.そこで、ξ1からξ4までの長さの和に定数Cをかけたものと||w||2との和を最小にするというのが最適化問題になる。
新しい最適化問題は以下のようになる:
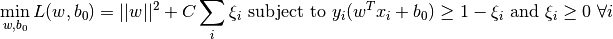
式中のパラメータCをどのように選ぶべきだろうか?その答えは学習データがどのように分布しているのかに依存している.一般的な答えは存在しないが以下の規則性を考慮するとよいだろう:
- Cの値を大きくすると誤分類を少なくできるが、マージンが小さくなってしまう.この条件下では、誤分類を起こすとコストが高くなることに注意.そもそも最適化の目的は項の値の最小化にあるため,誤分類はほとんど許容されなくなる。
- Cの値を小さくするとマージンが大きくなる一方、誤分類も増える.この条件下では、最小化に総和の項があまり寄与しないため,マージンの大きい超平面の発見に重きが置かれることになる.
補足資料¶
- NPTEL notes on Statistical Pattern Recognition, Chapters 25-29.
- Scikit-learn: Pythonの機械学習パッケージのサポートベクターマシンの項