SVMを使った手書き文字の文字認識¶
手書き数字の認識¶
k近傍法では,特徴ベクトルとして画素値を直接使った.今回は Histogram of Oriented Gradients (HOG)を特徴ベクトルとして使う.
ここではHOGを計算する前に,2次モーメントを使って画像の歪み補正を行う.それではまず初めに,数値画像を入力し歪み補正を行う deskew() 関数を定義しよう. 次が deskew() 関数の定義である:
def deskew(img):
m = cv2.moments(img)
if abs(m['mu02']) < 1e-2:
return img.copy()
skew = m['mu11']/m['mu02']
M = np.float32([[1, skew, -0.5*SZ*skew], [0, 1, 0]])
img = cv2.warpAffine(img,M,(SZ, SZ),flags=affine_flags)
return img
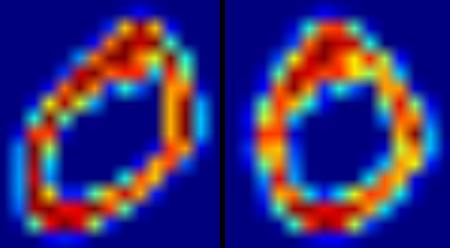
下図が、数字ゼロが書かれた画像に対しdeskew関数を適用した結果である.左の画像が原画像,右の画像が歪み補正された画像である.
次に各セルのHOG記述子を計算する.そのために,各セルに対してX, Y方向のSobelフィルタをかけ,各画素の勾配の方向と強度を計算する.この勾配は16個の整数値に量子化される.この画像を4個の小領域に分割する.各小領域に対して勾配強度によって重み付けされた勾配方向のヒストグラム(ビン数は16)を計算する.つまり,各章領域は16個の数値を持つベクトルを持つことになる.(4個の小領域に対して計算した)4個のベクトルは64個の数値を持つ特徴ベクトルとなる.これが我々のデータを学習するために使う特徴ベクトルになる.
def hog(img):
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1)
mag, ang = cv2.cartToPolar(gx, gy)
# ビン数(0...16)で量子化
bins = np.int32(bin_n*ang/(2*np.pi))
# 4個の小領域に分割
bin_cells = bins[:10,:10], bins[10:,:10], bins[:10,10:], bins[10:,10:]
mag_cells = mag[:10,:10], mag[10:,:10], mag[:10,10:], mag[10:,10:]
hists = [np.bincount(b.ravel(), m.ravel(), bin_n) for b, m in zip(bin_cells, mag_cells)]
hist = np.hstack(hists)
return hist
最後に,k近傍法を使った文字認識と同様,データセット(1個の大きな画像)を個別の画像に分割する.各数値に対して250個の画像を学習データ,残りの250個の画像をテストデータとする.全てのコードは以下のようになる:(注意: 画像はkNNのものと同じ, 下記のコードはpython2+OpenCV2用でOpenCV3では動かない。Python3+OpenCV3用はこれ)
import cv2
import numpy as np
SZ=20
bin_n = 16 # ビンの個数
svm_params = dict( kernel_type = cv2.SVM_LINEAR,
svm_type = cv2.SVM_C_SVC,
C=2.67, gamma=5.383 )
affine_flags = cv2.WARP_INVERSE_MAP|cv2.INTER_LINEAR
def deskew(img):
m = cv2.moments(img)
if abs(m['mu02']) < 1e-2:
return img.copy()
skew = m['mu11']/m['mu02']
M = np.float32([[1, skew, -0.5*SZ*skew], [0, 1, 0]])
img = cv2.warpAffine(img,M,(SZ, SZ),flags=affine_flags)
return img
def hog(img):
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1)
mag, ang = cv2.cartToPolar(gx, gy)
bins = np.int32(bin_n*ang/(2*np.pi)) # ビンを(0...16)で量子化
bin_cells = bins[:10,:10], bins[10:,:10], bins[:10,10:], bins[10:,10:]
mag_cells = mag[:10,:10], mag[10:,:10], mag[:10,10:], mag[10:,10:]
hists = [np.bincount(b.ravel(), m.ravel(), bin_n) for b, m in zip(bin_cells, mag_cells)]
hist = np.hstack(hists) # histは64ビットのベクトル
return hist
img = cv2.imread('digits.png',0)
cells = [np.hsplit(row,100) for row in np.vsplit(img,50)]
# 前半をtrainData, 後半をtestDataとする
train_cells = [ i[:50] for i in cells ]
test_cells = [ i[50:] for i in cells]
###### 学習中 ########################
deskewed = [map(deskew,row) for row in train_cells]
hogdata = [map(hog,row) for row in deskewed]
trainData = np.float32(hogdata).reshape(-1,64)
responses = np.float32(np.repeat(np.arange(10),250)[:,np.newaxis])
svm = cv2.SVM()
svm.train(trainData,responses, params=svm_params)
svm.save('svm_data.dat')
###### テスト中 ########################
deskewed = [map(deskew,row) for row in test_cells]
hogdata = [map(hog,row) for row in deskewed]
testData = np.float32(hogdata).reshape(-1,bin_n*4)
result = svm.predict_all(testData)
####### 制度を調査 ########################
mask = result==responses
correct = np.count_nonzero(mask)
print correct*100.0/result.size
この方法では93.9%の精度を実現した.SVMの様々なパラメータを調整して、より高い精度を実現してみよう.もしくはこの分野の論文を読んで、別の方法を実装してみよう.
補足資料¶
- Dalal,
N. & Triggs, B. (2005)
Histograms of Oriented Gradients Video. CVPR 2005 : YouTubeビデオ、 2012年公開