Rで統計学を学ぶ(3)
この講義では、教科書の第4章「母集団と標本」をとりあげます。
これは、大きな集団から一部を取り出した少数のデータの情報を用いて、
もとの集団の性質を推測する推測統計の基本的な理論の学習がねらいです。
特に 標本分布の理解を目的とします。
このウェブページと合わせて教科書を読み進めてください。
学習項目です
まず重要な用語をまとめておきましょう:
- 母集団: 対象のデータ全体
- 標本: 母集団から一部のデータを取り出した(抽出した)もの
- 標本抽出: 母集団から標本をとりだすこと
- 母数: 母集団の性質をあらわす統計的指数(比率、平均、分散、相関係数など)
例えば、日本の中学生全体のテスト得点データを母集団とすると、名古屋市昭和区の(一部の)中学生のテスト得点データが「標本」になります。そして、平均点や分散などが母数とみなせます。
手元にある標本から母集団の性質(母数)を推測することを推測統計といいます。
推測統計は推定と検定に分けられます。
「推定」は、母数の値に対し具体的な値を求める点推定、つまり一つの値で推定の結果を表すものと、区間推定、つまりある幅を持った区間で結果を表すものに分けられます。
また「検定」は母集団について述べた異なる立場の二つの主張(仮説)のうちどれを採用するかを決定するものです。例えば、日本の中学生のテスト得点が5年前と現在とで変化したという仮説と、変化していないという仮説がある場合、どちらを採択するかをきめるのが検定です。
母集団から抽出した標本を用いて、母数の点推定を行う手順についてみていきます。
ここで、標本のデータの個数のことを
サンプルサイズ、
もしくは
標本の大きさと言います。
例えば、10人の17歳男性の身長データがあるとします。これは日本人の17歳男性全体という『母集団』から抽出された『標本』とみなせます。そしてこのとき標本のデータの個数が10ですから、n = 10と書きます。ここでnはサンプルサイズを表す記号です。
身長 <- c(165.2, 175.9, 161.7, 174.2, 172.1, 163.3, 170.6, 168.4, 171.3)
この標本から、「17歳の日本人男性全体の身長」(母集団)の平均(母数の一つ)を点推定してみましょう。
それには、次のようにします。
mean(身長)
ここで
meanは、平均値を求めるRの関数でしたね。
まず用語を確認しましょう:
- 標本統計量:標本データから計算される平均や分散などの値
- 推定値:標本データを用いて計算した母数の推定量
母集団、標本、標本統計量、母数の関係を図で表すと以下のようになります: 母集団から抽出された標本データを分析し、標本統計量を得ます、それを使って母数を推定するのです

ここで、標本統計量からどのように母数を推定するかを表にしておきましょう:
| 母数 |
推定量 |
関係するRの関数 |
| 母平均 |
標本平均 |
mean |
| 母分散 |
不偏分散 |
var |
| 母標準偏差 |
不偏分散の正の平方根 |
sd |
| 母相関係数 |
標本相関係数 |
cor |
| 母比率 |
標本比率 |
prop.test |
課題3-1
前項で例に出した「身長データ」を用いて、母集団の分散と標準偏差を点推定した値を求めよ。
またそれに用いたRの関数をあわせて答えよ。
標本抽出に伴う誤差
標本から推定値を得る手順よりも大事なこと:
- 実際の母数の値にどの位近い推定値が得られるか?
- 推定の結果はどのくらい信用できるか?
- 標本誤差: 母数の値と推定値とのズレ---
データを沢山集めれば、生じうる誤差は小さくできる
- 標本分布: どのような推定値が得られる可能性があるか、についての手がかり
推定値の信頼性を調べる方法
推定値を計算する元になる、標本に含まれる「個々のデータの値」の決定方法について見ていきましょう。
- 標本抽出の方法---
単純無作為抽出と呼ばれる方法が前提
- 単純無作為抽出: 母集団の中のどのデータにも平等に選ばれる可能性を持っているような標本抽出の方法
- 無作為標本: 単純無作為抽出によって得られた標本
- 単純無作為抽出によって得られるデータの性質としての確率変数
- 確率変数: 実際に結果が得られるまでどのような値が得られるかが決まっていない変数
例: サイコロを振った時の出目
同じ手続でデータを得ても結果に再現性がない⇒
単純無作為抽出によって得られるデータは確率変数といえる
- 確率変数がどのような値をとるのかを示す確率分布
- 確率変数の実現値:抽出の結果、確率変数がとる値
- 確率分布: 確率変数がどのような値をどのような確率でとるかということを表した分布
[サイコロの出目の確率分布]
理論的には、サイコロの出目の確率分布はつぎのようになります:
| サイコロの出る目 |
1 |
2 |
3 |
4 |
5 |
6 |
| 確率 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
それに対し、次のシミュレーションにより、サイコロの出る目の度数分布は次のようになりました:
set.seed(1)
dice6times <- ceiling(runif(6,0,6))
table(dice6times)
size=60000
dice60000times <- ceiling(runif(size,0,6))
table(dice60000times)
table(dice60000times)/(size/6)
(1) 6回サイコロを振った場合:
| サイコロの目 |
1 |
2 |
3 |
4 |
5 |
6 |
| 度数 |
0 |
2 |
1 |
1 |
0 |
2 |
| 相対度数 |
0 |
2/6 |
1/6 |
1/6 |
0 |
2/6 |
(2) 60,000回サイコロを振った場合:
| サイコロの目 |
1 |
2 |
3 |
4 |
5 |
6 |
| 度数 |
10,097 |
9,918 |
9,936 |
9,960 |
10,050 |
10,039 |
| 相対度数 |
1.0097 |
0.9918 |
0.9936 |
0.9960 |
1.0050 |
1.0039 |
このように、非常に多くの実現値が得られれば、度数分布は確率分布とほぼ同じになります
- 確率分布を用いた母集団の表現としての母集団分布
- 母集団分布:ある変数の母集団における分布
無作為抽出の場合、標本データの確率分布は母集団分布と同じになります
- 代表的な母集団分布である正規分布
- Rを使って正規分布の母集団から標本を抽出する方法
正規分布(normal distribution, ガウス分布 Gaussian distributionともいう)は統計学で最もよく用いられる確率分布なので、ここで復習しておこう
正規分布の表現方法: N (μ,σ2) --- μは平均値、σ2は分散 (σは標準偏差)

正規分布のグラフの書き方:
curve(dnorm(x,mean=0,sd=1), from=-4, to=4)
curve(dnorm(x,mean=1,sd=1), add=TRUE)

|

|
| 正規分布 N (0,1)のグラフ |
正規分布 N (1,1) のグラフを重ね書き |
- 標準正規分布: 平均0 分散1の正規分布 --- N(0,1)
- 離散変数: 整数など、とびとびの値をとる変数(例:サイコロの出目)
- 連続変数: 実数値をとる変数(例:正規分布に従う確率変数)
- 確率密度 : 正規分布の図の縦軸は確率密度
確率密度×確率変数の範囲=確率
- 確率密度関数:確率密度を確率変数の値の関数として表したもの
正規分布の性質:
- μ-σからμ+σ の範囲(偏差値で言えば、40点から60点の範囲)の確率はおよそ 0.683
- μ-2σからμ+2σ の範囲(偏差値で言えば、30点から70点の範囲)の確率はおよそ 0.954
- μ-3σからμ+3σ の範囲(偏差値で言えば、20点から80点の範囲)の確率はおよそ 0.997

|

|

|
| μ-σからμ+σ の範囲 | μ-2σからμ+2σ の範囲 | μ-3σからμ+3σの範囲 |
[
正規分布グラフに領域を表示する関数]
正規分布グラフに領域を表示するためのRの関数を参考としてあげておきます:
hnorm <- function(range, color) {
plot(dnorm, -4, 4)
xvals <- seq(-range, range, length=30)
dvals <- dnorm(xvals)
polygon(c(xvals, rev(xvals)), c(rep(0,30), rev(dvals)), col=color)
abline(v=0, lty=2)
abline(v=-range, lty=3)
abline(v=range, lty=3)
abline(h=0, lty=2)
}
正規母集団から単純無作為抽出を行う
正規母集団から単純無作為抽出を行う場合、特にサンプルサイズが小さいと、
確率変数が正規分布に従っているかどうかは標本データのヒストグラムを見てもわからない(左図)。
しかし大きなサイズになれば、ほぼ正規分布に従うことわかる(右図).
> 標本 <- rnorm(n=5,mean=50,sd=10)
> 標本
[1]59.87265 55.41718 34.19793 52.95355 59.10080
> hist(標本)
> 大標本 <- rnorm(n=10000,mean=50,sd=10)
> hist(大標本)

|

|
| 標本(n=5) |
大標本(n=10000) |
標本分布とは、標本統計量(標本平均、標本分散など)に関する確率分布のこと
標本分布は標本における個々のデータの実現値を表した度数分布ではなく、標本統計量の確率分布
標本分布は母集団分布と標本統計量の種類、そしてサンプルサイズが決まると理論的(数学的)に導かれる。
実際のデータから作成されるわけではない
標本分布から何がわかるのか
標本分布を調べることで、推定値の性質が分かる可能性がある
標本分布を調べるときの観点:
- 標本分布が母数の本当の値を中心として分布しているか⇒平均
- 標本分布が横に大きく広がっていないか⇒標準偏差
(1)が満たされないと推定値と母数との誤差が大きくなる
(2) は推定値にどの程度誤差が生じるか調べるもの
標本分布を「経験的」に求める
Rを用いて「経験的」に標本分布を求める方法---「経験的」とは「現実に得られたデータに基づく」という意味、
理論的な標本分布を「近似的」に再現
母集団からサンプルサイズnの標本を何度も繰り返し抽出し、そのたびに標本統計量の実現値を計算して記録する
これを実行するときの問題
- 母集団分布がどのような分布になるかが不明
- 母集団分布がわからないと、標本から得られる推定値の信頼性も不明
⇒ 母集団が正規分布であると仮定して「もし母集団分布がこのような正規分布ならば、このくらいあてになる推定値が得られる」ということを検討
正規母集団の母平均の推定
仮定:母集団分布は
N (50,10
2)、 サンプルサイズ n =10
> 標本 <- rnorm(n=10,mean=50,sd=10)
> 標本
[1] 43.17949 39.07841 51.59838 44.00960 42.78063 53.01545
[7] 47.99463 48.81240 46.76994 65.39066
> mean(標本)
[1] 48.26296
この結果、母平均の推定値は 48.3
[
48.26296 なのに答は 48.3?]
注意: 48.26296 と表示されたとしても、答として、これをこのまま答えないこと。
有効数字の桁数を考慮して、48.3と答える(有効数字は2桁、計算途中なので3桁とする)。
母平均は50なので、推定値との差は 1.7 --- この差が標本誤差(誤差)
一回きりの標本抽出で推定値がどれくらいの誤差をもつかは、いろいろ
先の操作を10000回繰り返してみよう:
標本平均 <- numeric(length=10000)
for( i in 1:10000 ){
標本 <- rnorm(n=10,mean=50,sd=10)
標本平均[i] <- mean(標本)
}
こうして得られた標本平均のヒストグラムと母集団の正規分布とを、次のコードにより重ねあわせてみると、かなり近い関係にあることが分かります:
hist(標本平均, freq=FALSE)
curve(dnorm(x,mean=50,sd=sqrt(10)),add=TRUE)
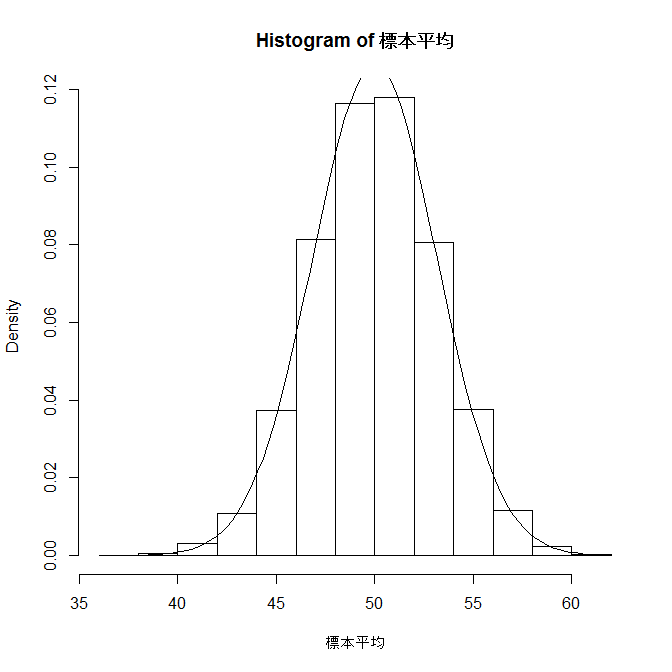
平均μ、分散σ
2の正規分布
N (μ, σ
2)に従う母集団からサンプルサイズnの標本を抽出したとき、
標本平均の標本分布は、理論的にN (μ, σ2/n) に従います。
誤差の絶対値が5以下、すなわち母平均の推定値が45以上、55以下の範囲で得られた回数を調べてみましょう:
> 誤差絶対値5以下 <- ifelse(abs(標本平均 - 50) <= 5, 1, 0)
> table(誤差絶対値5以下)
誤差絶対値5以下
0 1
1167 8833
全体の88%は本当の母数±5に収まっていることがわかります。理論的にはこのデータは
N (50,10)に従うので、次章の知識を先取りしRの関数pnormを用いた理論的な値と比較してみましょう:
> pnorm(55, mean=50, sd=sqrt(10)) - pnorm(45,mean=50,sd=sqrt(10))
[1] 0.8861537
このように、 上位二桁まで一致していることが確かめられました。
平均μ、分散σ2の正規分布 N (μ, σ2)に従う母集団からサンプルサイズnの標本を抽出したとき、標本平均の標本分布は、理論的にN (μ, σ2/n) に従うことは、次のようにして実験的に確かめることができます。
for ( k in c(50,60,70,80,90,100,150,200,250,300) ) {
標本平均 <- numeric(length=10000)
for( i in 1:10000 ){
標本 <- rnorm(n=k,mean=50,sd=10)
標本平均[i] <- mean(標本)
}
cat("サンプルサイズ=",k," 平均=",mean(標本平均),
"分散=",var(標本平均)*(k-1)/k, "母分散/分散=",
100/(var(標本平均)*(k-1)/k), "\n")
}
この実行結果は以下のようになります:
サンプルサイズ= 50 平均= 49.99211 分散= 1.949846 母分散/分散= 51.2861
サンプルサイズ= 60 平均= 50.00122 分散= 1.633351 母分散/分散= 61.22382
サンプルサイズ= 70 平均= 50.02179 分散= 1.416551 母分散/分散= 70.59402
サンプルサイズ= 80 平均= 49.97832 分散= 1.235205 母分散/分散= 80.95824
サンプルサイズ= 90 平均= 50.01785 分散= 1.114071 母分散/分散= 89.76091
サンプルサイズ= 100 平均= 49.99396 分散= 0.9985369 母分散/分散= 100.1465
サンプルサイズ= 150 平均= 49.9866 分散= 0.667744 母分散/分散= 149.758
サンプルサイズ= 200 平均= 50.00681 分散= 0.499225 母分散/分散= 200.3105
サンプルサイズ= 250 平均= 50.00481 分散= 0.3976698 母分散/分散= 251.4649
サンプルサイズ= 300 平均= 50.00694 分散= 0.3322331 母分散/分散= 300.9935
サンプルサイズを変えても標本平均の平均が母平均にほぼ一致すること、また
標本平均の分散は、母分散/サンプルサイズであることが確かめられました。
不偏性
ある推定量の標本分布の平均が、推定しようとしている母数の値と一致するとき、その推定量は不偏性があるといいます。また、
不偏性がある推定量のことを不偏推定量と言います。
推定量の不偏性は「標本分布が母数の本当の値を中心として分布しているか」に対応した概念です。
「推定量の標本分布の標準偏差(へんさ)」を
標準誤差(ごさ)と言います。
これは「標本分布の横への広がり」を表す値です。標準誤差が小さいということは、
標本分布の広がりが小さいことを表し、これは『ばらつきが少ない』ことを意味します。
例: N (50, 102)の正規母集団から n=10 の標本を抽出したとき、
標本平均の標本分布はN(50, 102/n)に従うので、標準誤差はsqrt(n)、つまり(n=10なので) およそ3.2となります。
ということは、標本平均から母集団の平均を推定しようとすると、おおよそ68%の確率で46.8から53.2の間の値が得られますが、運が悪いと5以上の誤差が生じることがあることがわかります。
この例から、(1)母集団の分散(母分散)が大きければ大きいほど標本の平均値は母平均から離れた値を取りやすい(標準誤差が大きくなりやすい)、(2)標本のサイズが小さいほど標準誤差が大きい、ということがわかります。
言い換えれば、標準誤差を小さくするにはサンプルサイズnを大きくするのが有効な方法であると言えます。
一般に、どのような標本統計量でも、サンプルサイズが大きいほど標準誤差は小さくなります
中心極限定理: 母集団が正規分布でなくとも、標本平均の標本分布は「サンプルサイズnが大きい時」はほぼ正規分布になる
課題3-2
標本分布を求めるの項目ではn=10の標本を10000個作り、その標本平均を求めた。
この課題ではn=100として10000個の標本平均を求めてみよう。そしてn=10の場合のヒストグラムとn=100の場合のヒストグラムを比較し、標準誤差が小さくなっていることを確かめてみよ。
[
ヒント]
n=10のときの標本平均が変数 SampleAverage10に入っており、
n=100のときの標本平均が変数 SampleAverage100に入っているとする。
この2つのヒストグラムを重ねあわせ表示するには、x軸とy軸をともに合わせる必要がある。
それには次のように xlim と ylim の値を指定すればよい:
hist(SampleAverage10, col="yellow", xlim=c(35, 65), ylim=c(0,2500))
par(new=T)
hist(SampleAverage100, col="green", xlim=c(35, 65), ylim=c(0,2500))
その結果、以下の様な図が表示される:

標本平均以外の標本分布
「平均」以外の母数のうち、分散と中央値の標本分布について述べます。
標本分散と不偏分散の標本分布
母分散の推定量としての標本分散と不偏分散の違いを実験で示しましょう。
標本分散 <- numeric(length=10000)
不偏分散 <- numeric(length=10000)
for ( i in 1:10000 ){
標本 <- rnorm(n=10,mean=50,sd=10)
標本分散[i] <- mean((標本-mean(標本))^2)
不偏分散[i] <- var(標本)
}
> mean(標本平均)
[1] 89.74351
> mean(不偏分散)
[1] 99.71502
> sd(標本分散)
[1] 42.25119
> sd(不偏分散)
[1] 46.94577
> hist(標本分散, breaks=seq(0,500,10))
> hist(不偏分散, breaks=seq(0,500,10))

|

|
| 標本分散のヒストグラム | 不偏分散のヒストグラム |
- 不偏分散は不偏性をもつという点では望ましい性質をもっているが、
標本分散に比べて過大な推定値が得られる可能性が高い
- 不偏分散の平方根は母標準偏差の不偏推定量ではない
中央値の標本分布
実験: 標本中央値の標本分布を求め、標本平均と比較する(どちらが母平均の推定量としてよいか?)
標本平均 <- numeric(length=10000)
標本中央値 <- numeric(length=10000)
for(i in 1:10000) {
標本 <- rnorm(n=10,mean=50,sd=10)
標本平均[i] <- mean(標本)
標本中央値[i] <- median(標本)
}
> mean(標本平均)
[1] 49.97365
> mean(標本中央値)
[1] 49.95716
> sd(標本平均)
[1] 3.147899
> sd(標本中央値)
[1] 3.716859
標準誤差が最小
> hist(標本平均)
> hist(標本中央値)

|

|
| 標本平均のヒストグラム | 標本中央値のヒストグラム |
| 目的 |
関数名と書式 |
使い方 |
| 小数点以下を切り上げ |
ceiling(a) |
ceiling(1.5) ⇒ 2 |
| 一様分布に従う乱数の発生 |
runif(n,min,max) |
runif(n=10, min=0, max=6) ⇒
0から6までの範囲の一様乱数を10個生成 |
| 決まったパターンの乱数の生成(乱数の『種』の指定) |
set.seed(seed) |
set.seed(1) ⇒
乱数の種を1に設定。これを指定すると常に同じパターンの乱数が生成される |
| 棒グラフの作成 |
barplot(height,names.arg) |
barplot(c(2/3, 1/3), names.arg=c("男性","女性"))
⇒ 高さ2/3, 1/3の棒に『男性』『女性』のラベルをつける |
| 関数の曲線を描く |
curve(func, from, to) |
curve(dnorm(x), from=-3, to=3)
⇒ 標準正規分布を描く
|
| 正規分布の確率密度関数 |
dnorm(x,mean,sd)
| dnorm(0,mean=0,sd=1)
⇒ 標準正規分布におけるx=0のときの確率密度
|
| 正規分布に従う乱数の発生
| rnorm(n,mean,sd)
| rnorm(n=10,mean=50,sd=10)
⇒ N(50,102)に従う乱数を10個生成
|
| 数値を格納する場所の確保 |
numeric(length)
| a <- numeric(length=10000)
⇒ 変数aに数値データを10,000個格納できるようにする
|
| 連続データを作る |
a:b
| x <- 0:20
⇒ 0から20までの整数の連続データを作り変数xに格納
|
| 同じ処理の繰り返し |
for(i in データ) { 処理 } |
for(i in 1:100) { cat("hello, world!\n") }
⇒ { }内の処理を100回繰り返す: hello, world!が100回表示される
|
問題3-1
教科書p.107 (1): N (50, 102)の正規母集団からn = 20の標本抽出を5,000回繰り返すことにより、標本平均の経験的な標本分布を求めよ。またこの経験的な標本分布からえられるグラフ(ヒストグラム)に、理論的に導かれる標本分布を重ねあわせて表示せよ。(注意: 経験的な標本分布のヒストグラムを書くとき、freq=FALSEを指定すること)
[ヒント]
標本平均データを作るには、
標本分布を求めるの項目で学んだように、次のようにすれば良い:
標本平均 <- numeric(length=5000)
for (i in 1:5000){
標本 <- rnorm(n=20,mean=50,sd=10)
標本平均[i] <- mean(標本)
}
このヒストグラムは、後で正規分布のグラフと重ね合わせるため
freq=FALSEの指定が必要である(freqは「頻度(度数, frequency)」を表す。ヒストグラムは度数を表示するのがデフォルトである。それに対し正規分布は確率密度関数なので、度数では表現されない)
また、これに重ね合わせる理論的な正規分布は、
N (50, sd
2)となる。ここでsdの値は、母集団の標準偏差の10
ではなく、
標準誤差の項目で学んだように、サンプルサイズを考慮した値にしなければならない。
この結果下のようなグラフが得られる:

問題3-2
教科書p.107 (2): 理論的な標本分布について、サンプルサイズをn=1, 4, 9, 16, 25と変化させた時に、標本分布の形状がどのように代わるかを調べてみよ。ただし、母集団分布は標準正規分布N (0, 12)とする。
[ヒント]
幾つもの図を重ねあわせるには、次のようにfor 文を使えば良い。
for (n in rev(c(1,4,9,16,25))) {
curve( ここに適切なコードを書く ,add=TRUE)
}
これによって得られた図が下。なお、上のコードで rev を使わないと、図の上が切れてしまうことに注意:

問題3-3
最小値0、最大値100の一様分布からn=20の標本抽出を5,000回繰り返すことにより、標本平均の経験的な標本分布を求めよ。中心極限定理からこれは正規分布に近づくはずである。そこでこのヒストグラムに、標本平均データの平均と標準偏差による正規分布のグラフを重ねせて表示せよ(注意: 経験的な標本分布のヒストグラムを書くとき、freq=FALSEを指定すること)
[ヒント]
ここで用いる乱数発生の関数が runif であること以外は、問題3-1と同じようにしてできる。
この結果、次のようなグラフが得られる:

Rで統計学(2) トップページに戻る Rで統計学(4)

















